24. Structure and Bonding of Boron Carbide
Despite belonging to the class of very hard materials and thus offering a high potential for applications, detailed knowledge of the structure of boron carbide is limited due to the very similar neutron and x-ray scattering cross sections of the constituent atoms and the complexity of the crystal structure. At the same time, this complexity is a severe obstacle to mapping out the full energy landscape. The present application note describes how cluster expansion can be used in combination with ab initio calculations based on density functional theory (DFT) to thoroughly map the energy landscape thereby resolving the issue and allowing for a deeper understanding of the chemical bonding of this exciting material.
Keywords: boron carbide, carbides, hardness
24.1. Background
Boron carbide, B4C, is one of the hardest materials known, close to diamond and cubic boron nitride. Due to these mechanical properties it is used in many applications as an abrasive or shielding material. In nuclear power reactors boron carbide is used to control the neutron flux due to the high neutron absorption of 10B and the radiation hardness and chemical stability of B4C. According to the boron-carbon phase diagram proposed by Elliott, which is reproduced in Figure 24.1.1, a boron carbide phase exists between approximately 9 at% to 20 at% C with a melting point reaching 2450 °C, which is complemented by carbide phases with excess boron and graphite, respectively, below and above this carbon concentration range [2].
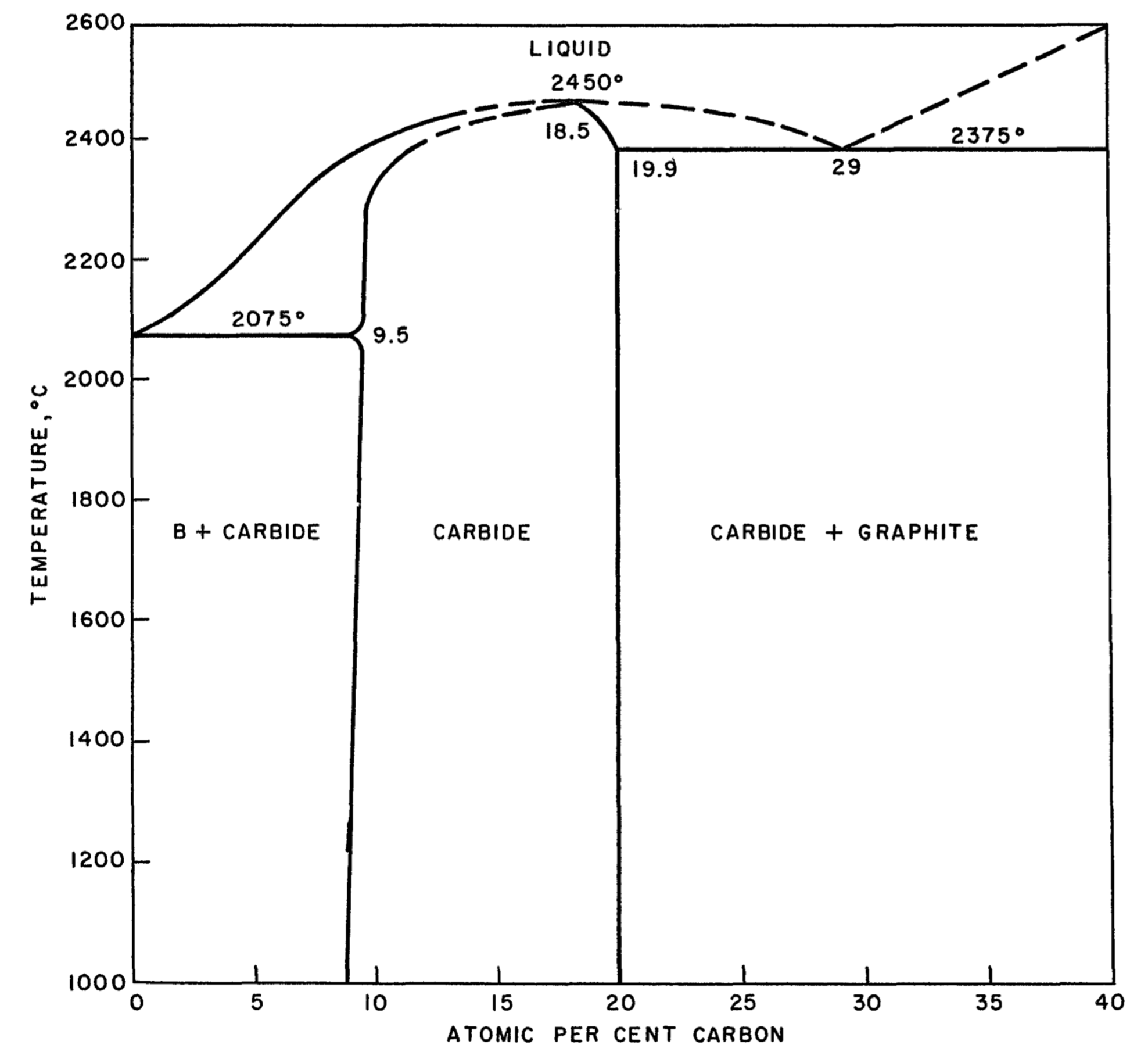
Figure 24.1.1 Boron-carbon phase diagram as reported by Elliott [2].
The crystal structure of boron carbide is characterized by a rhombohedral lattice with a single icosahedron at the corner and a three-atom linear rod parallel to the hexagonal c axis at the center of the unit cell with lattice parameters of about a = 5.6 Å and c = 12.1 Å in hexagonal setting. While Larson obtained for both B4C and boron-rich B13C2 a C-B-C arrangement within the rods from x-ray diffraction data and, hence, boron-pure icosahedra as shown in Figure 24.1.2 for the latter compound [3], Clark and Hoard gave a structure for B4C with linear C-C-C rods and again icosahedra comprised of only B atoms [4].
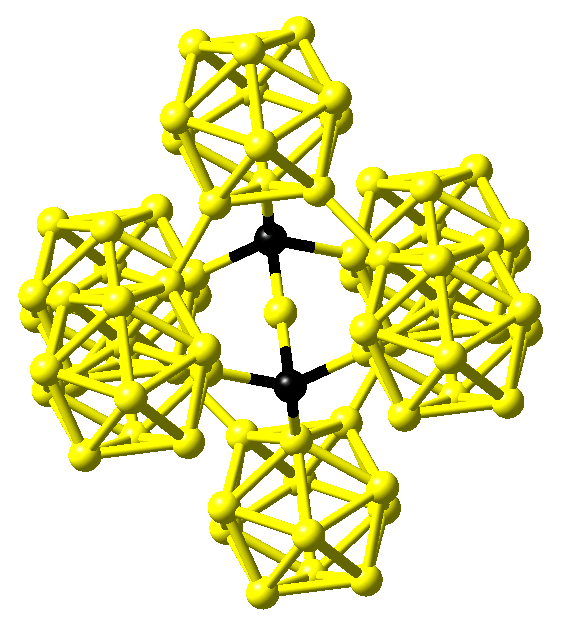
Figure 24.1.2 Structure of B13C2as proposed by Larson [3]. Boron and carbon atoms are shown in yellow and black, respectively.
In contrast, comparing infrared absorption and Raman diffusion measurements to the predictions of ab initio calculations for B4C, Lazzari et al. confirmed the finding of linear C-B-C rods reported by Larson but in addition were able to identify the carbon atom within the B11C icosahedra at the polar sites, which form the top and bottom triangles [5]. This structure is shown in Figure 24.1.3.
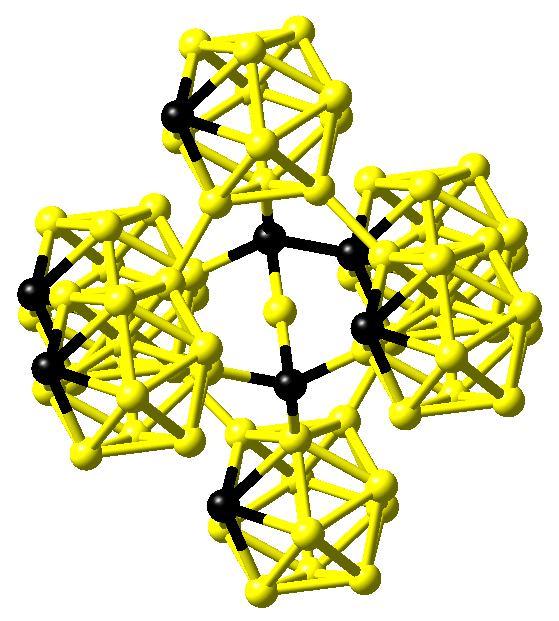
Figure 24.1.3 Structure of B4C as proposed by Lazzari et al. [5]. Boron and carbon atoms are shown in yellow and black, respectively.
The same result was obtained by Mauri et al., who compared the results of their ab initio calculations to 13C and 11B NMR chemical shifts [6]. However, these groups considered only small sets of ordered structures.
The present application note goes beyond all previous approaches by applying the cluster expansion approach in combination with ab initio calculations to unambiguously determine the distribution of the atoms within the structure by scanning hundreds of thousands of structures for energetical stable configurations.
24.2. Method of Calculation
Cluster expansion is a method describing the energy of a system as a function of the distribution of the atoms on the lattice [7] [8]. In a nutshell, as indicated in Figure 24.2.1 it is based on expressing a desired quantity such as energy as an expansion of contributions from clusters of various size with 1, 2, 3, … vertices.
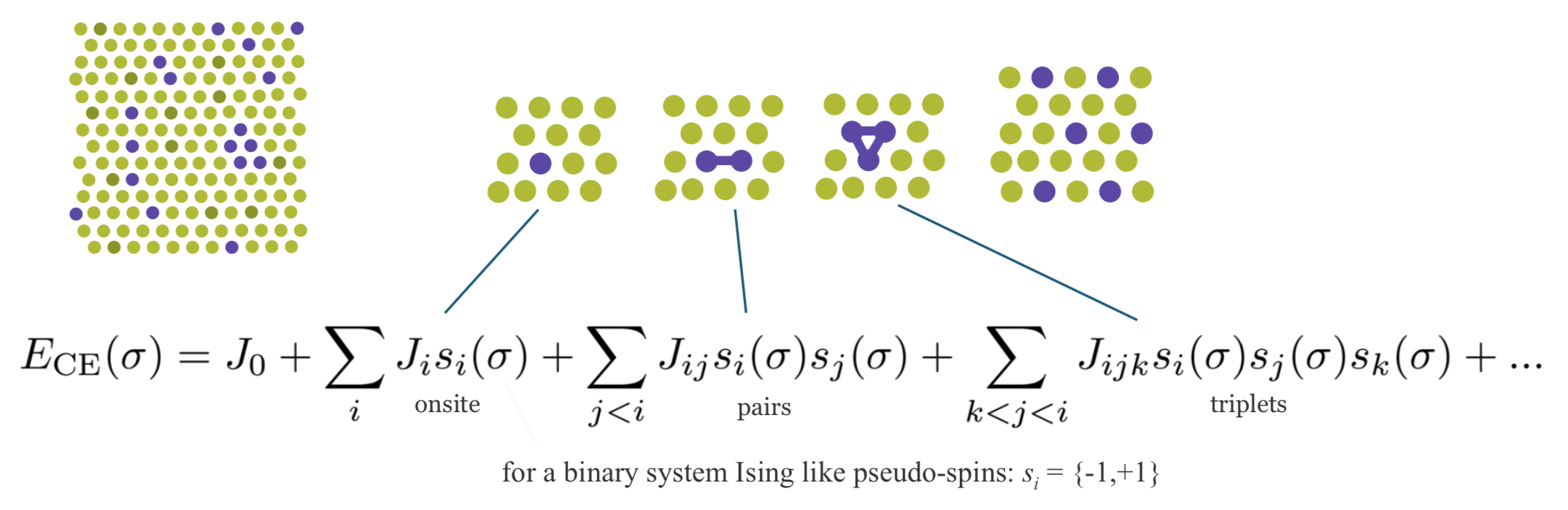
Figure 24.2.1 Schematic description of the cluster expansion method.
Any crystal structure can be decomposed into a near to infinite set of clusters with different length and composed of different numbers of vertices, i.e., two-body interactions, three-body interactions etc. An effective interaction parameter J is assigned to each of these clusters to reproduce the correct energy (or any other desired quantity). The core task in cluster expansion is to truncate the cluster set to a reasonable size and to identify the correct effective interaction parameters. The universal cluster expansion code UNCLE [8] uses a genetic algorithm to identify an optimum set of clusters with their corresponding interaction parameters based on a training set of structures. The energies of the training set structures are calculated by using MedeA VASP. Structures are iteratively added to the training set as sketched in Figure 24.2.2.
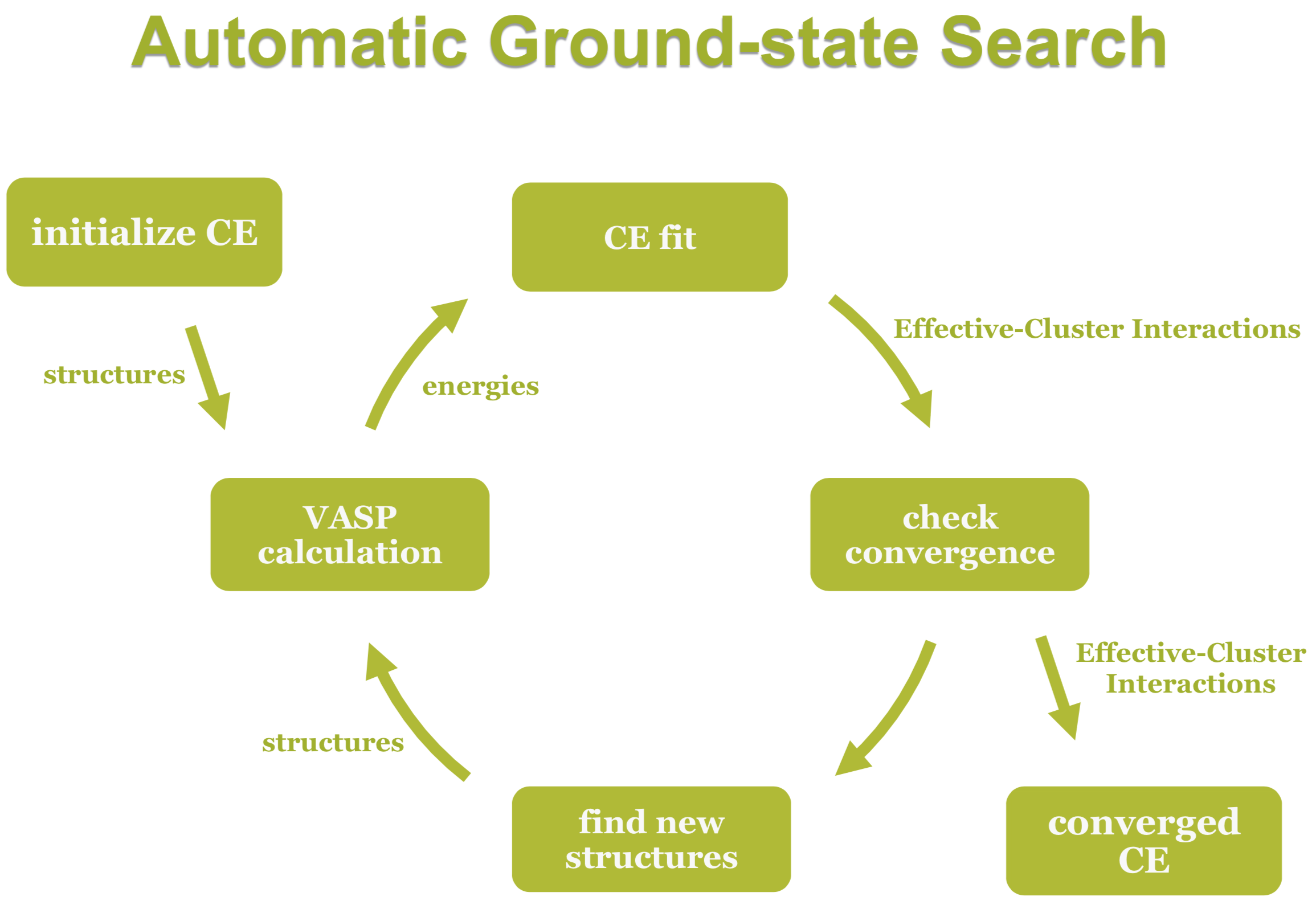
Figure 24.2.2 Schematic description of the cluster expansion method.
Within the MedeA computational environment this approach is made available via MedeA UNCLE. The DFT calculations are performed using MedeA VASP [9], which uses projector augmented (PAW) potentials and wave functions [10]. For the present application note, exchange and correlation effects were included within the semilocal GGA as parametrized by the PBE scheme [11]. All structures were fully relaxed.
24.3. Computed Results
The results obtained from the cluster expansion calculations for the boron-carbide system are summarized in Figure 24.3.1, which shows enthalpies of formation for boron carbides with five different boron concentrations. In order to achieve convergence, 63 DFT calculated structures using up to two unit cells were added to the training set. Based on this training set effective cluster interactions were obtained and used to predict the energies of 838511 structures with DFT accuracy.
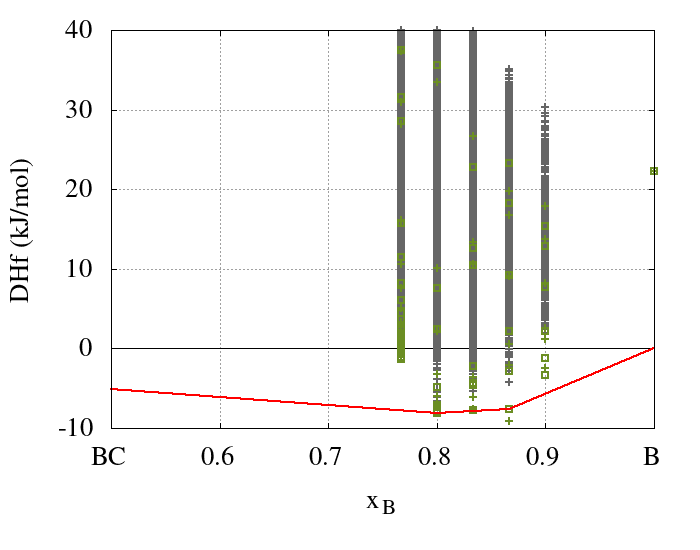
Figure 24.3.1 Ground-state diagram of a binary cluster expansion of boron carbide. The DFT caculated enthalpies of formation of the training set structures are marked by green squares while their CE predicted enthalpies are indicated by green crosses. The CE predicted enthalpies of all other structures, not included in the training set, are marked by gray crosses. The red line indicates the convex hull of the enthalpies of formation as obtained with DFT.
The results obtained from the cluster expansion confirm the previous findings. However, since the cluster expansion takes all disordered structures fully into account at the ab initio level, the present results are much more general. Specifically, the ground-state structures obtained for B13C2(xB = 0.866) and B4C (xB = 0.8) are identical to those proposed by Larson, Lazzari et al., and Mauri et al. shown in Figures 24.1.2 and 24.1.3, which share the linear C-B-C motifs, whereas additional carbon atoms prefer the polar sites of the icosahedra.
With the ground-state structures for different boron concentrations at hand the elastic and vibrational properties of these compounds are readily calculated with the help of the MedeA MT and MedeA Phonon modules. The elastic coefficients as computed using a fully automated, symmetry general approach [12] and summarized in Figure 24.3.2 reveal considerable stiffening of the material with increasing C concentration between B9C and B4C in nice agreement with the lowering of the enthalpy of formation within this sequence.
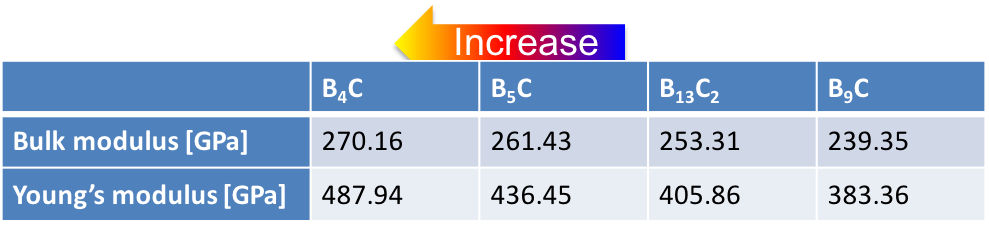
Figure 24.3.2 Computed elastic coefficients of boron carbides with boron concentration between xB = 0.8 and xB = 0.9.
Finally, the computed phonon dispersions for B4C confirm the thermodynamic stability of this compound and reveal an isolated high-frequency mode, which originates from bond-stretching vibrations of the B atoms in the C-B-C linear rods as illustrated in Figure 24.3.3, which is consistent with the analysis of Lazzari et al. [5].
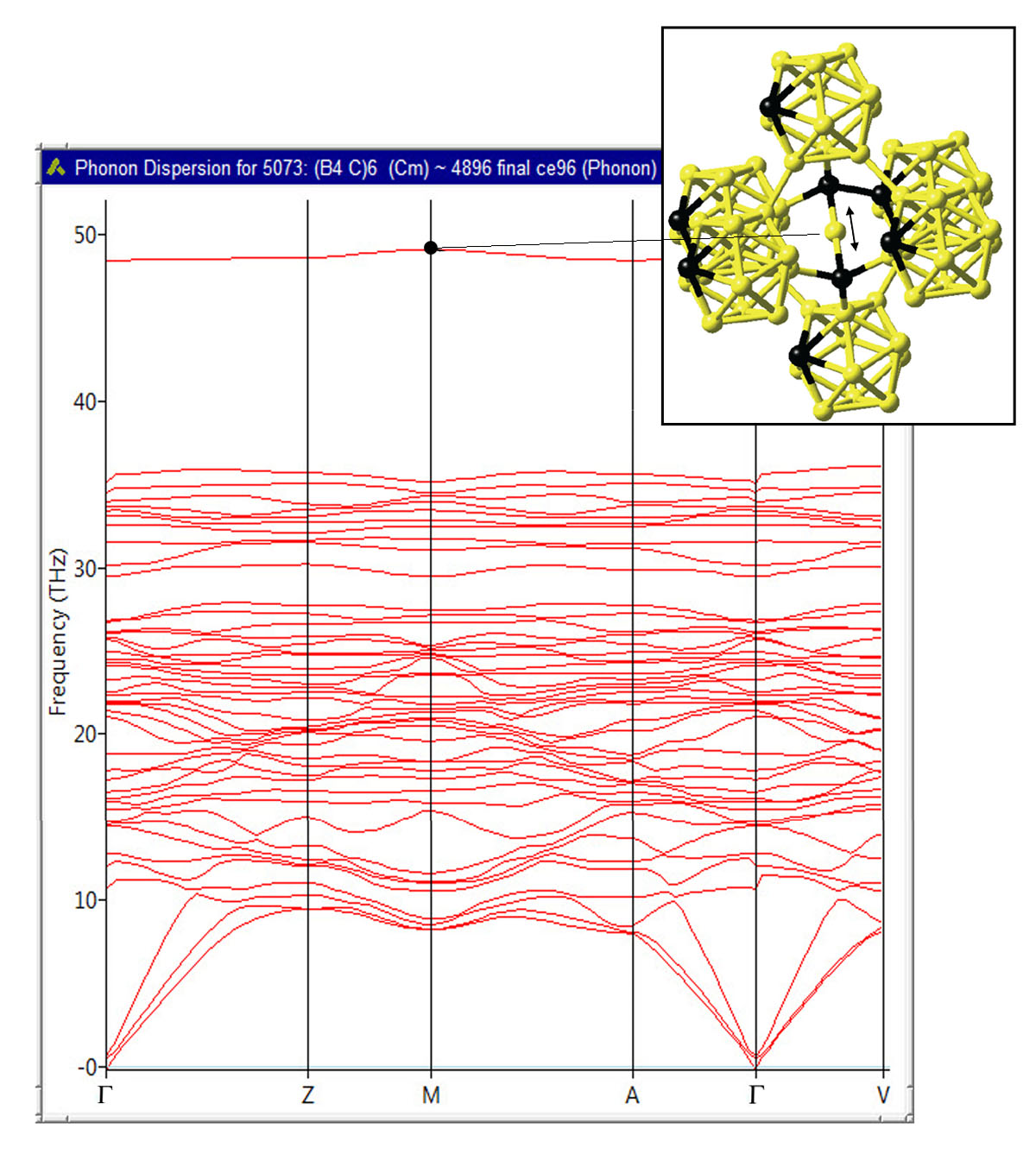
Figure 24.3.3 Computed phonon dispersion of B4C. The high-frequency mode at 48 THz corresponds to the bond-stretching vibrational mode of the B atoms in the C-B-C linear rods as indicated by the arrow shown in the inset.
24.4. Conclusion
In this project cluster expansion in combination with DFT simulations has been employed to predict the ground-state structures of boron carbides with boron concentrations varying between xB = 0.8 and xB = 0.9. Whereas due to the similar neutron and x-ray scattering cross sections of B and C detailed knowledge about the positions of these atoms within the complex structures was missing and previous computations considered only small sets of ordered structures, the present approach goes beyond by including disordered structures from the outset. For B4C and B13C2the investigation confirms the C-B-C sequence of the linear rods, whereas additional carbon atoms in B4C prefer the polar sites of the icosahedra. Computed elastic properties show a stiffening of boron carbide with increasing carbon concentration, while analysis of vibrational spectra reveals a high-frequency mode connected to bond-stretching within the linear rods.
MedeA modules used in this application
- MedeA Environment
- MedeA VASP
- MedeA UNCLE
- MedeA MT
- MedeA Phonon
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | (1, 2) R. P. Elliott, “The Boron-Carbon System”, ARF 2200-12 (Final Technical Report), May 1, 1960 – April 30, 1961, Illinois Institute of Technology 1961 (DOI) |
| [3] | (1, 2) A. C. Larson, “Comments concerning the crystal structure of B4C”, in “Boron-Rich Solids”, edited by D. Emin, T. Aselage, C. L. Beckel, I. A. Howard, and C. Wood, AIP Conf. Proc. 140, 109 (1986) (DOI) |
| [4] | H. K. Clark and J. L. Hoard, “The Crystal Structure of Boron Carbide”, J. Am. Chem. Soc. 65, 2115 (1943) (DOI) |
| [5] | (1, 2, 3) R. Lazzari, N. Vast, J. M. Besson, S. Baroni, and A. Dal Corso, “Atomic Structure and Vibrational Properties of Icosahedral B4C Boron Carbide”, Phys. Rev. Lett. 83, 3230 (1999) (DOI) “Erratum: Atomic Structure and Vibrational Properties of Icosahedral B4C Boron Carbide, [Phys. Rev. Lett. 83, 3230 (1999)]”, Phys. Rev. Lett. 85, 4194 (2000) (DOI) |
| [6] | F. Mauri, N. Vast, and C. J. Pickard, “Atomic Structure of Icosahedral B4C Boron Carbide from a First Principles Analysis of NMR Spectra”, Phys. Rev. Lett. 87, 085506 (2001) (DOI) |
| [7] | J. M. Sanchez, F. Ducastelle, and D. Gratias, “Generalized Cluster Description of Multicomponent Systems”, Physica A 128, 334 (1984) (DOI) |
| [8] | (1, 2) D. Lerch, O. Wieckhorst, G. L. W. Hart, R. W. Forcade, and S. Müller, “UNCLE: a code for constructing cluster expansions for arbitrary lattices with minimal user-input”, Modelling Simul. Mater. Sci. Eng. 17, 055003 (2009) (DOI) and references therein |
| [9] | G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”, Phys. Rev. B 54, 11169 (1996) (DOI); “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set”, Comput. Mater. Sci. 6, 15 (1996) (DOI) |
| [10] | P. E. Blöchl, “Projector augmented-wave method”, Phys. Rev. B 50, 17953 (1994) (DOI). |
| [11] | J. P. Perdew, K. Burke, and M. Ernzerhof, “Generalized Gradient Approximation Made Simple”, Phys. Rev. Lett. 77, 3865 (1996) (DOI); “Erratum: Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]” Phys. Rev. Lett. 78, 1396 (1997) (DOI) |
| [12] | Y. Le Page and P. Saxe, “Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress”, Phys. Rev. B 65, 104104 (2002) (DOI) |
| download: | pdf |
|---|