34. Prediction of ideal heat capacity, Cp,id(T), of alkanolamines and amides: a combined QM – QSPR approach
Keywords: heat capacity, alkanolamines, QM, QSPR, MOPAC
34.1. Introduction
In process engineering, heat capacity is an important property that determines the amount of energy to provide to a system to raise its temperature. However, there is not yet a group contribution approach that allows prediction of heat capacity with temperature. The variations of heat capacity with temperature are influenced by the quantification of the vibrational energy levels [2] [3]. This is probably why empirical approaches are subject to difficulties. In the ideal gas state, these variations can be reliably predicted by quantum chemistry methods [4]. In the liquid or dense gas state, the prediction is a combination of an ideal contribution and a residual contribution [5]: \(C_{p}(T,P) = C_{p,id}(T) + C_{p,res}(T,P)\), where the ideal gas heat capacity \(C_{p,id}(T,P)\) is the main term containing vibrational, transitional, and rotational contributions, and the residual term \(C_{p,res}(T,P)\) is predicted using classical statistical mechanics or equations of state [6].
The present application note illustrates the high throughput capabilities of MedeA [1] to predict ideal heat capacity of a substantial list of amides and alkanol amines in a large temperature range (200-1,000 K). The results are then used to parametrize a new functional form for \(C_{p,id}(T,P)\) allowing fast prediction and improved physical relevance for engineering applications. For instance, the new functional form is consistent with the continuously increasing trend of \(C_{p,id}(T,P)\) and has the expected asymptotic limit. An original QSPR approach is developed to parametrize the new expression.
34.2. Method and protocol
The list of compounds is assembled by retrieving SMILES strings from internet sources, namely, Wikipedia, NIH, and NIST. A structure list is then created in MedeA by reading a text file of names and SMILES strings. In order to sample the possible shapes, the structure list contains up to ten stable conformers per compound, which are built by exploring different sequences of dihedral torsion angles. Each conformer of the list is structurally optimized using MedeA MOPAC with the semi-empirical PM7 method and a vibrational analysis is performed. The heat capacity is computed and printed for a list of regularly spaced temperatures gathered in a property table in the Job.out file of the task, together with the enthalpy of formation and entropy. The structure list comprises 36 species (Figure 34.2.1). For each molecule, the lower energy conformer is identified and its vibrational analysis is checked for the absence of imaginary vibration frequencies. A corresponding property table is printed out for each species and used to develop new QM-based correlations or compare with existing correlations (for instance those from DIPPR).
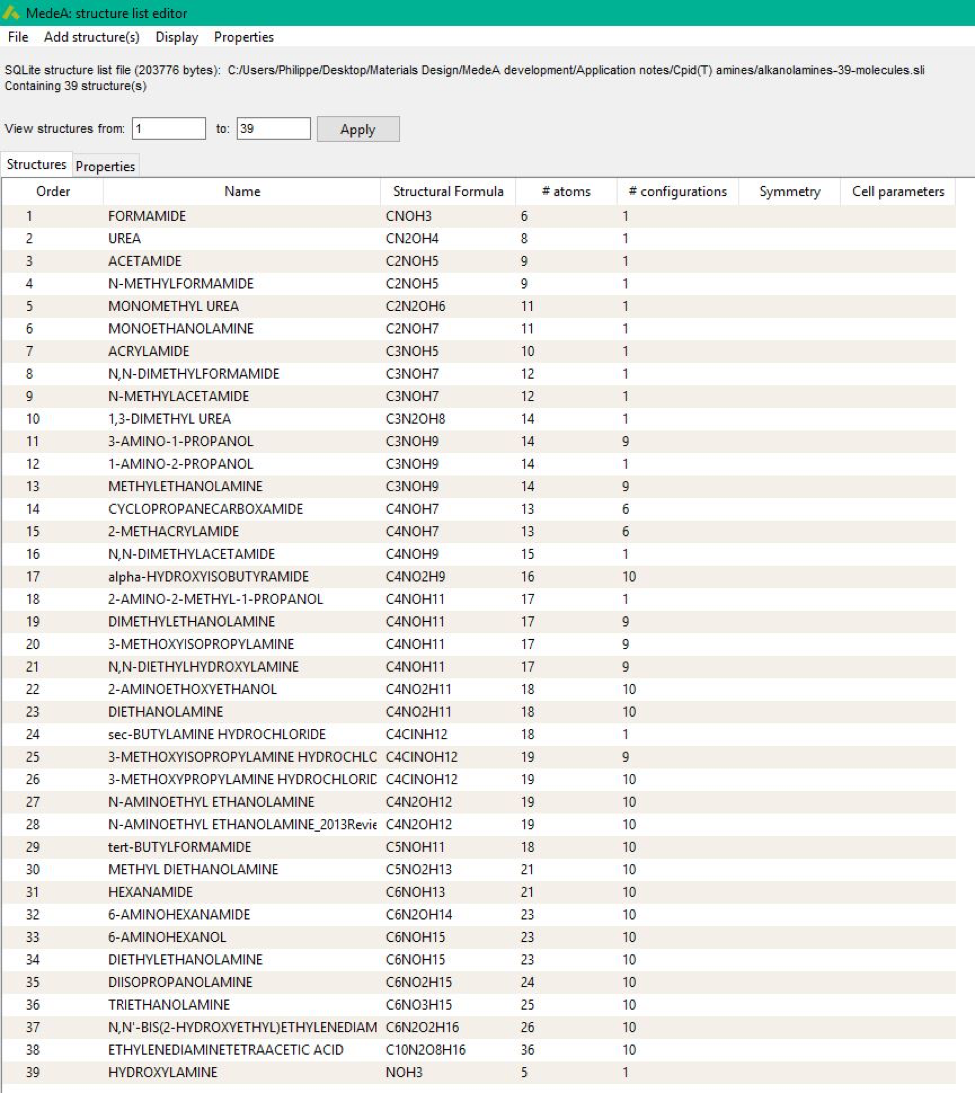
Figure 34.2.1 Names and formulas for the training set of 36 compounds.
In the present work, we use the following functional form for \(C_{p,id}(T,P)\):
where A, B, C, D, and E are theory-derived or empirical parameters.
If we set \(\theta_{\nu 1} = 2C\) and \(\theta_{\nu 2} = 2E\), the above equation is exactly equivalent to the heat capacity of an ideal gas of polyatomic molecules with two characteristic vibrational temperatures \(\theta_{\nu 1}\) and \(\theta_{\nu 2}\) [2]. The parameter B or D is the degeneracy (i.e. the weight) of each vibrational frequency. The parameter A is the ideal heat capacity in the limit of low temperature (translational + rotational contributions):
The number of rotational degrees of freedom is p = 2 for a linear molecule and p = 3 for a non-linear molecule. Another constraint is the asymptotic value in the limit of high temperatures, which corresponds to a contribution of R/2 per vibrational degree of freedom (in application of the equipartition of energy):
where n is the total number of atoms. The model outlined in Equations (1) - (3) has certainly important limitations, e.g., it does not account for possible conformational changes, although it maintains a low number of independent parameters (three), thus making their regression more reliable. It is also ensuring a safe behavior in the low and high temperature limits. It may be noted that Equation (1) is close from the equation used in DIPPR to correlate \(C_{p,id}(T,P)\), the only difference being that DIPPR contains a term \(cosh(E/T)\) instead of \(sinh(E/T)\). This may lead to some artifacts at high temperature (see Appendix for more details and references about this equation).
34.3. Results
A standard flowchart of MedeA MOPAC for thermodynamic property prediction is applied to the structure list of 39 amines and amides of Figure 34.2.1, which contain 0 to 20 carbon atoms. The list includes primary, secondary, tertiary, and quaternary cyclic or branched amines and amides.
MedeA MOPAC helped finding ground state structure for each molecule, with the exception of one hydrochlorinated amine which would require an improved initialization. The training set contains 38 compounds, including two hydrochlorinated amines. Thermodynamic properties are printed for temperatures between 308 and 808 K with a value each 10 K.
In a first step, the optimization for the parameters B, C, D, and E is done separately for each compound.
The parameter A = 33.26 J mol-1 K-1 is identical for all compounds, as the set contains non-linear molecules exclusively. B and D parameters increase with molecular size, as expected. The parameter C ranges between 300 and 500 K, while most compounds exhibit values between 300 and 400 K. The parameter E ranges from 1150 to 1450 K. These values correspond to \(\theta _{\nu 1} = 2C\) between 600 and 1000 K, and \(\theta _{\nu 2} = 2E\) between 2300 and 2900 K, i.e., within the expected range of characteristic vibrational temperatures.
In a second step, we correlate parameters A, B, C, D, and E with selected descriptors. In Figure 34.3.1, the parameter B appears to vary linearly with the total number of atoms with a regression coefficient of 0.97.
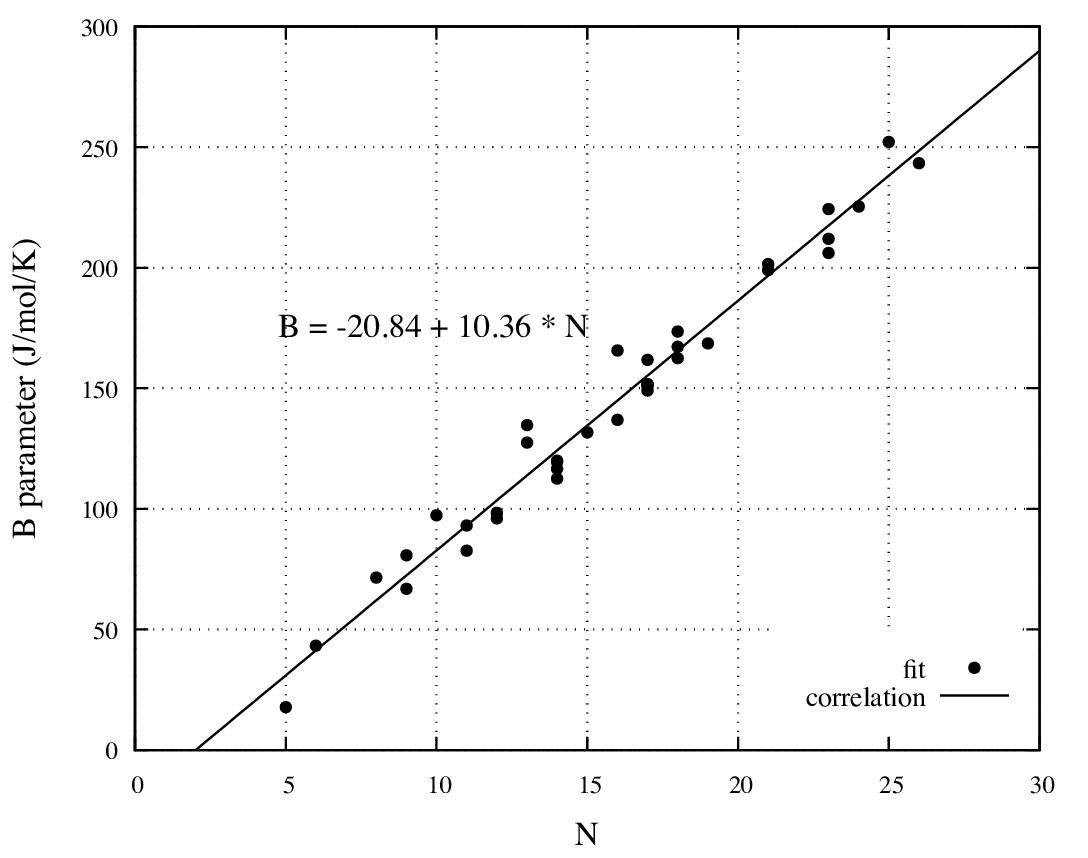
Figure 34.3.1 Variation of parameter B of Equation (1) with the total number of atoms for the 36 amines of Figure 34.2.1.
The parameter D correlates best with the number of hydrogen atoms nH (Figure 34.3.2). The regression coefficient is 0.99.
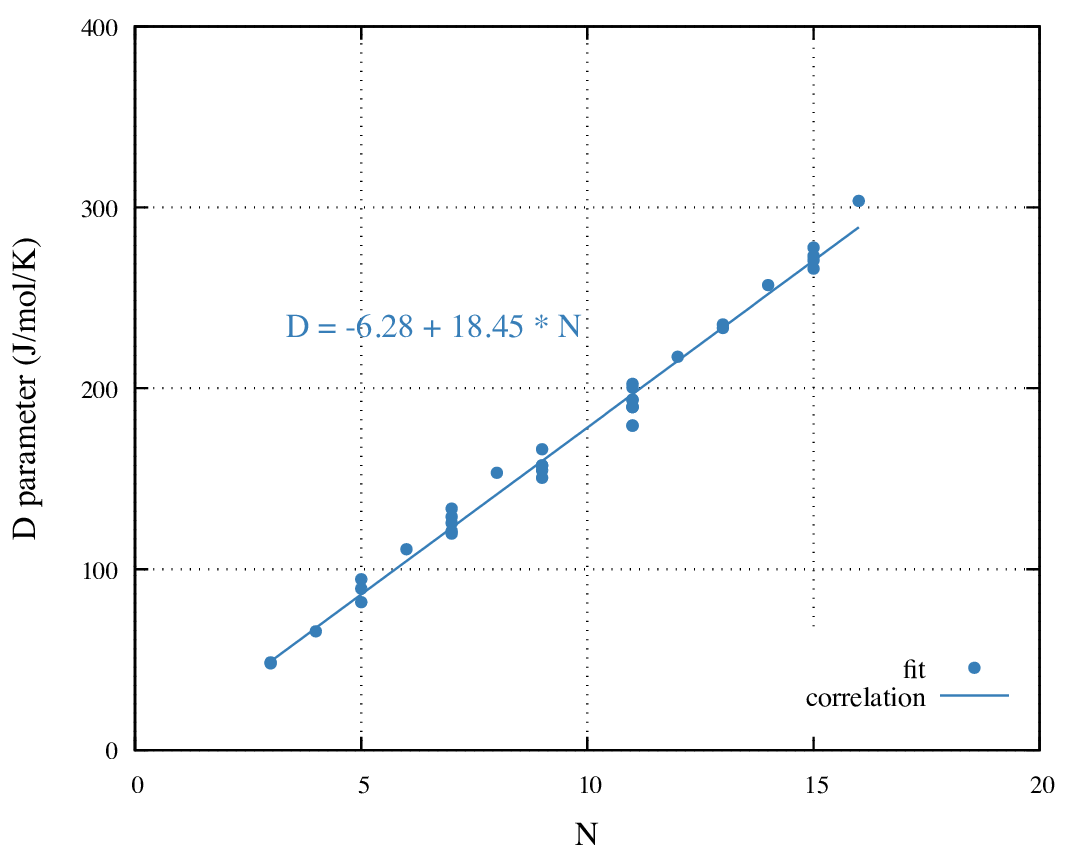
Figure 34.3.2 Variation of parameter D of Equation (1) with the number of hydrogen atoms for the 36 amines of Figure 34.2.1.
The parameters C and E also vary regularly, yet they change faster for small carbon numbers. They correlate linearly with \(\dfrac{1}{n_{H}}\) (Figure 34.3.3).
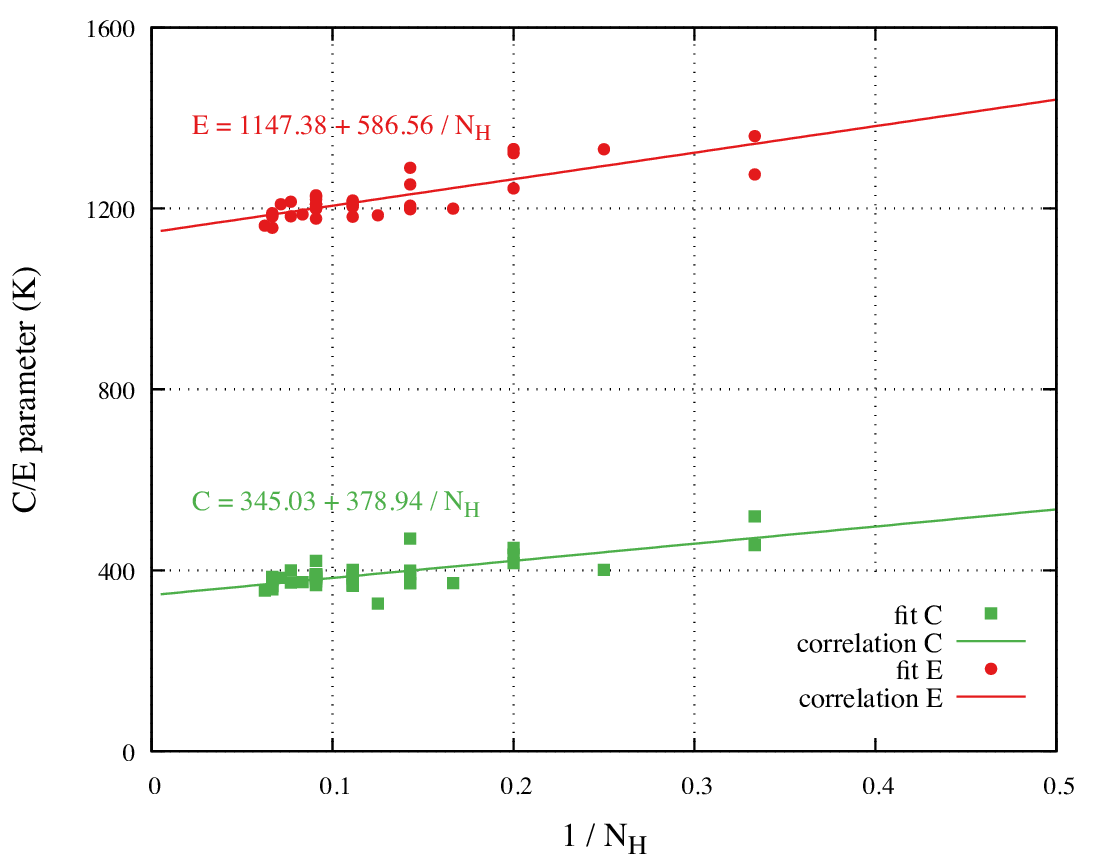
Figure 34.3.3 Variation of parameters C and E of Equation (1) with the inverse number of hydrogen atoms.
The functional forms suggested by Figures 34.3.1 and 34.3.3 are:
An outline of results is indicated for a few selected compounds in (Figure 34.3.4).
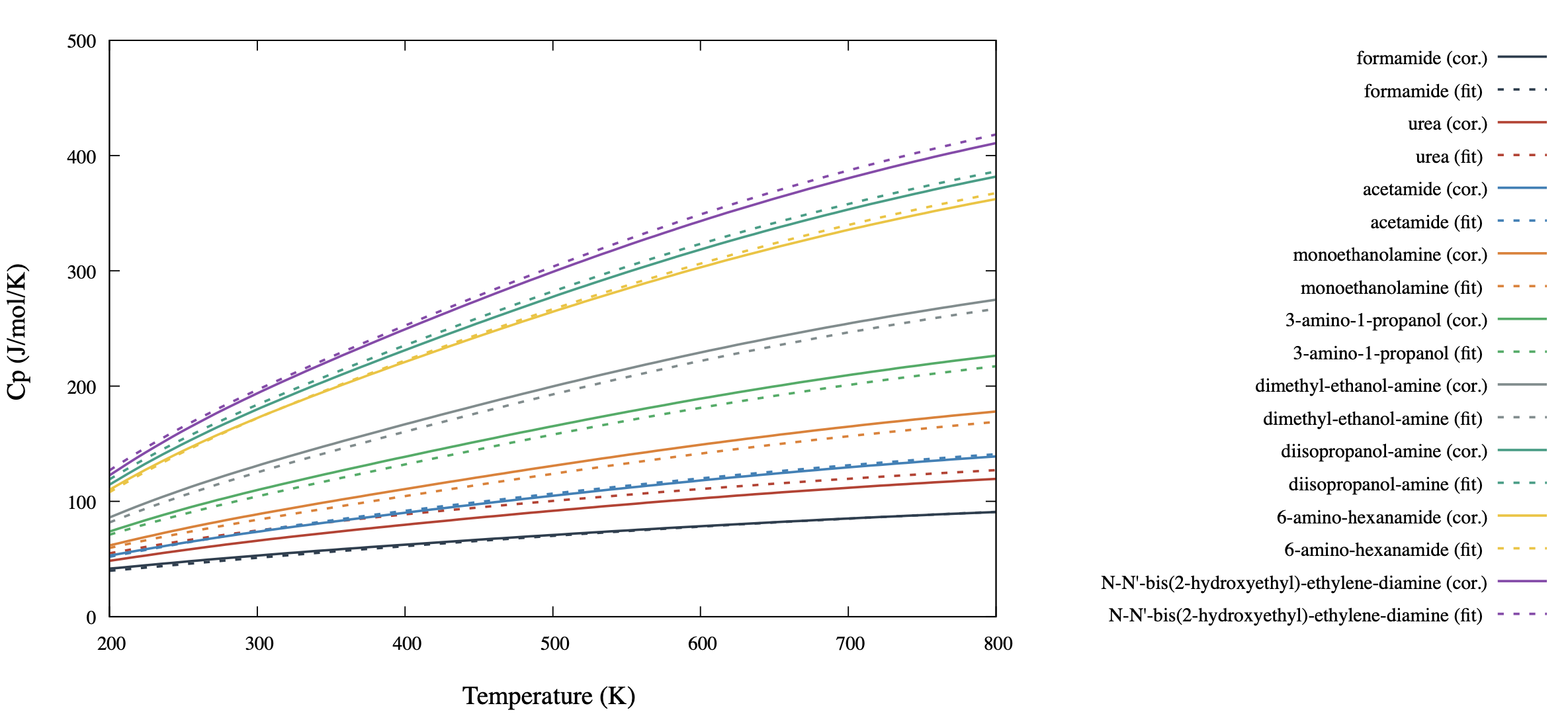
Figure 34.3.4 Selected results of ideal gas heat capacity prediction for alkanol amines and amides belonging to the training set of 36 molecules.
34.4. Conclusions
The proposed functional form involving two vibrational frequencies (Equation (1)) allows parametrization from QM results covering the relevant range for most engineering applications (308-808 K). The main advantages are:
(i) each parameter has a physical meaning given by quantum mechanics, ensuring consistent extrapolation to high and low temperatures,
(ii) the stable optimization protocol involves only three parameters per pure compound, hence not resulting in additional computation cost for the end-user compared with DIPPR equations,
(iii) the regressed parameters vary regularly in homogeneous series, allowing to build predictive correlations for \(C_{p,id}(T,n_{C})\), and
(iv) the approach can be extended to ideal gas energy and entropy with theoretical expressions from [2].
The proposed methodology presents a substantial improvement compared with previous methods (e.g. Benson’s method), which are not based on explicit QM calculations with vibrational analysis. It is also a substantial progress compared to experiment-based correlation work (e.g. DIPPR project, Poling’s textbook [7]), which predict sometimes unrealistic \(C_{p,id}(T)\) at high temperature. Further improvement is still possible by increasing the number of parameters, for instance, introducing a third vibration frequency in Equation (1) or additional descriptors, or adding the effect of possible chemical transformations or conformational changes, and testing correlations with an independent validation dataset.
Appendix
The equation provided by Mc Quarrie (1976) for a polyatomic gas is:
where k is the Boltzmann constant, N is the Avogadro number. The number of rotational degrees of freedom is p = 2 for a linear molecule and p = 3 for a non-linear molecule. The index j runs over the vibrational degrees of freedom, and \(\vartheta_{\text{vj}}\) is the characteristic vibrational temperature associated with the jth vibrational degree of freedom.
If we introduce \(C_{j} = \ \frac{\vartheta_{\text{vj}}}{2}\), considering that \(C_{p,id}-C_{v,id} = R = N*k\) for an ideal gas, Equation (8) rearranges into:
If the summation is simplified assuming two frequencies, we obtain Equation (1). We can compare it with the Equation that correlates with the ideal heat capacity, \(C_{p,id}(T)\) in DIPPR:
In Equation (10), the term:
is consistent with theory (Equation (1)), and the last term
is not. A more detailed analysis shows a decrease of the vibrational contribution when temperature increases up to several thousand K.
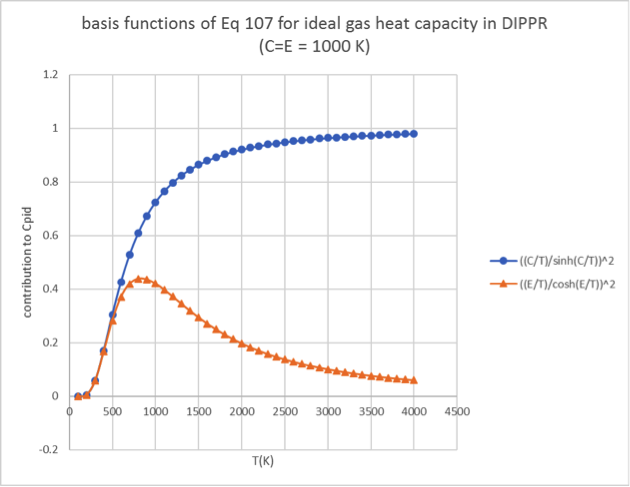
Figure 34.4.1 Comparison of the two terms \(\left\lbrack \frac{\frac{C}{T}}{\sinh\left( \frac{C}{T} \right)} \right\rbrack^{2}\) and \(\left\lbrack \frac{\frac{E}{T}}{\cosh\left( \frac{E}{T} \right)} \right\rbrack^{2}\) with temperature in Equation (1). The constants C and E are set to 1000 K in this example.
Required MedeA modules
- MedeA GUI
- MedeA HT module (structure lists, conformer analysis)
- MedeA MOPAC (semi-empirical molecular QM, structural optimization, vibrational analysis, thermodynamic property determination)
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | (1, 2, 3) D. A. McQuarrie, (1976), “Statistical Mechanics”, New York, Harper and Collins, New revised edition, (2000). |
| [3] | S. W. Benson, “Thermochemical kinetics”, New York, Wiley, (1976). |
| [4] | X. Rozanska, J. J. P. Stewart, P. Ungerer, B. Leblanc, C. Freeman, P. Saxe, and E. Wimmer, “High-throughput calculations of molecular properties in the MedeA environment: Accuracy of PM7 in predicting vibrational frequencies, ideal gas entropies, heat capacities, and Gibbs free energies of organic molecules”, J. Chem. Eng. Data 59, 3136 (2014) (DOI). |
| [5] | M. Yiannourakou, P. Ungerer, B. Leblanc, N. Ferrando, and J.-M. Teuler, “Overview of MedeA®-GIBBS capabilities for thermodynamic property calculation and VLE behaviour description of pure compounds and mixtures: application to polar compounds generated from ligno-cellulosic biomass”, Mol. Simul. 39, 1165 (2013) (DOI). |
| [6] | M. Lagache, P. Ungerer, A. Boutin, and A. H. Fuchs, “Prediction of thermodynamic derivative properties of fluids by Monte Carlo simulation”, Phys. Chem. Chem. Phys. 3, 4333 (2001) (DOI). |
| [7] | B. E. Poling, J. M. Prausnitz, and J. P. O’Connell, “The properties of gases and liquids, 5th edition”, New York, McGraw Hill, (2001). |
| download: | pdf |
|---|