8. Change of Elastic Properties of Graphite Electrode upon Li Intercalation
Keywords: Graphite, anode, lithium ion battery, elastic properties, first-principles, computations
First-principles calculations reveal a three-fold increase in the Young’s modulus of graphite as it is fully lithiated (C + Li \(\rightarrow\) Li@C). Based on the calculations we determined a linear expression that describes the approximate stiffness of Li@C as a function of Li loading which may lead to greatly improved continuum models of electrode deformation and failure.
Keywords: Graphite, anode, lithium ion battery, elastic properties, first-principles, computations
8.1. Background
Graphite is currently being used as state-of-the-art anode material in Li ion batteries (LIB’s). As such, there is a critical need for an in-depth understanding of fundamental graphite properties at the varying operating conditions of a device. Upon charging of a battery cell with a graphite anode, Li cations of the electrolyte are intercalated as Li atoms between the graphene sheets. This electrochemical lithium intercalation occurs in stages following a sequence of dilute stage 1, stage 4, stage 3, liquid-type stage 2, stage 2, and stage 1 compounds. [1] The stage number relates to the number of graphene layers between two lithium layers. In the dilute stage 1, lithium randomly occupies the available sites between graphene layers. In the liquid type stage 2 compounds of nominal composition LiC18 are formed (left image of Figure 8.1.1). In the highly ordered stage-2, structures with the stoichiometry LiC12 exist and the stage-1 structure has the composition LiC6 (see other structures of Figure 8.1.1).
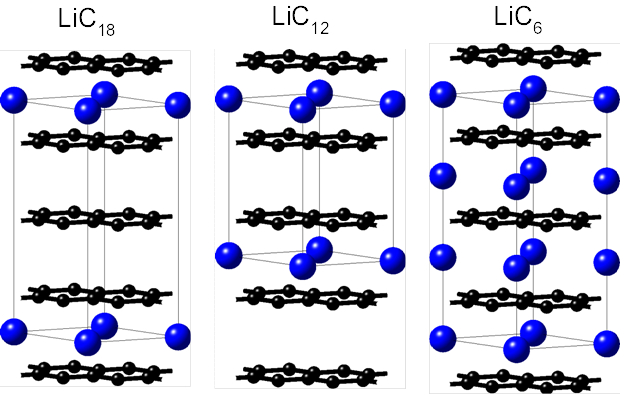
Figure 8.1.1 Crystal structures of Li-intercalation compounds. Black and blue spheres represent atoms of C and Li, respectively. The thin solid black lines outline the unit cells.
Overall the formation of LiC6 is accompanied by a 10% increase in volume compared to pure graphite. [2] The significant changes in structure and bonding due to repeated Li diffusion in and out of the anode have significant effect on the elastic properties and can lead to structural failure. We performed first-principles calculations to determine the elastic properties as the Young’s moduli (E) and Poisson’s ratios (\(\nu\)) for pure Li and graphite, respectively, and graphite at different lithium loading levels representative of the phases formed during the cycling of an LIB. [1] With a linear correlation between the Li loading levels and the calculated changes of the elastic properties we developed an engineering-scale model of the anode deformation and fracture.
8.2. Computational Approach
We calculated the elastic properties wth the MedeA MT module [3] using the bcc crystal structure of metallic Li, pure graphite, and the crystal structues of LiC18, LiC12, and LiC6, respectively (see Figure 8.1.1). With MedeA MT the calculations are straightforward and fully automated and can be combined with first-principles methods as implemented in MedeA VASP. [4]
8.3. Computed Results
The calculated structural parameters of the systems that are shown in Figure 8.1.1 are consistent with experimental measurements. [5] [6] Even the 10% volume increase upon lithiation can be well captured with the calculations. The computed Young’s moduli (E) and Poisson’s ratios for polycrystalline Li@C systems, along with graphite and metallic lithium are presented in Table 8.3.1.
| System | Young’s modulus E (GPa) | Poisson’s ratio |
|---|---|---|
| Graphite | 32.5 | 0.32 |
| LiC18 | 28.6 | 0.39 |
| LiC12 | 58.1 | 0.34 |
| LiC6 | 108.7 | 0.24 |
| Li | 2.0 | 0.34 |
It is intriguing that LiC6 has a Young’s modulus which is more than three times larger than that of graphite. The softest compound is lithium metal followed by graphite and LiC18, whereby the two latter systems have similar Young’s moduli. With increased Li content \(n_{Li}\) the Young’s modulus increase almost linearly in the sequence LiC18 \(\rightarrow\) LiC12 \(\rightarrow\) LiC6. Based on the computed results, the Li content \(n_{Li}\) and the Young’s moduli of Li@C compounds follow an approximate linear relationship
suitable for use in continuum-scale models of electrode deformation.
8.4. Significance
Since graphite is widely used as a lithium battery anode, you should understand the change in the elastic response during charging and discharging. This is a critical step in improving the accuracy of engineering models of electrode design. First-principles computations reliably predict elastic properties of materials and empower engineers to complete experimental data with a high level of confidence. In particular, you can use MedeA to predict the mechanical properties of battery materials under wide-ranging conditions to provide insight into the underlying physical mechanisms that lead to stress, deformation and eventual structural failure.
Required MedeA modules
- MedeA Environment
- MedeA JobServer and TaskServers
- MedeA Pearson
- MedeA VASP
- MedeA MT
| [1] | (1, 2) Y. F. Reynier, R. Yazami, and B. Fultz, “Thermodynamics of Lithium Intercalation into Graphites and Disordered Carbons”, J. Electrochem. Soc. 151, A422 (2010) DOI |
| [2] | (1, 2) Y. Qi, H. Guo, L.G. Hector Jr., and A. Timmons, “Threefold Increase in the Young’s Modulus of Graphite Negative Electrode during Lithium Intercalation”, J. Electrochem. Soc. 157, A558 (2010) DOI |
| [3] | Y. Le Page and P. Saxe, “Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress”, Phys. Rev. B 64, 104104 (2002) DOI |
| [4] | G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”, Phys. Rev. B 54, 11169 (1996) DOI and “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set”, Comput. Mater. Sci. 6, 15 (1996) DOI |
| [5] | D. Billaud, F.X. Henry, M. Lelaurain, and P. Willmann, “Revisited structures of dense and dilute stage II lithium-graphite intercalation compounds”, J. Phys. Chem. Solids 57 775 (1996) DOI |
| [6] | T. Yao et al., “Analysis of layered structures of lithium–graphite intercalation compounds by one-dimensional Rietveld method”, Solid State Ionics 175 199 (2004) DOI |
| download: | pdf |
|---|