11. Elastic coefficients and moduli for silicon carbide (\(\beta\)‑SiC), corundum (\(\alpha\)-Al2O3), and ferric tourmaline (schörl)
The high predictive power of first-principles calculations is demonstrated with the calculation of elastic coefficients and moduli for cubic silicon carbide, \(\beta\)-SiC, corundum, \(\alpha\)-Al2O3, and ferric tourmaline, schörl, with a fairly complex crystal structure.
Keywords: Mechanical properties, elastic coefficient, silicon carbide, corundum, schorl
11.1. Background
The response to external mechanical deformations determined by for example the compressive and tensile strength or the resistance to shear belong to the most important properties of materials playing a central role in mechanical engineering at the macroscopic level as well as at the nanoscale. Yet, accurate measurement of these properties can be quite tedious and thus experimental data are often unknown or blurred by rather large experimental errors. For example, the experimental values of the shear modulus of cubic silicon carbide found in the literature vary between 27.5 GPa and 160.0 GPa [2], [3]. In contrast, first-principles calculations of these fundamental mechanical properties give values comparable to experimental data, but at substantially smaller effort and cost. In the present application note, this is demonstrated for cubic silicon carbide, \(\beta\)-SiC, corundum, \(\alpha\)-Al2O3, and ferric tourmaline, schörl, which has a fairly complex crystal structure. For these compounds the elastic coefficients and the elastic moduli (bulk, Young’s, and shear modulus) are calculated and compared to experimental data.
11.2. Method of Calculation
Elastic properties are calculated in the MedeA ®[1] MT module by straining structures and evaluating the resulting stresses [4]. This easy to use and fully automated tool can be combined with classical or first-principles methods. In the present application note MedeA MT is used with the latter, first-principles method based on density functional theory as performed with MedeA VASP [5] using projector-augmented (PAW) potentials and wave functions [6].
11.3. Computed Results
11.3.1. Silicon carbide
The crystal structure of cubic \(\beta\)-SiC with space group \(F\bar{4}3m\) is displayed in Figure 11.3.1.1. Crystals with such a space group have three independent elastic coefficients, C11, C12, and C44, from which the elastic moduli are derived.
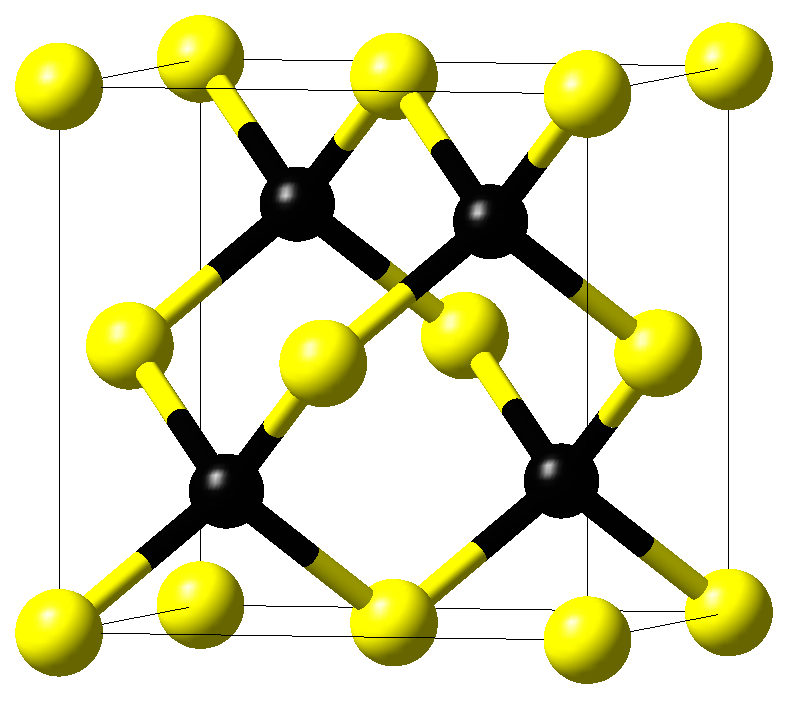
Figure 11.3.1.1 Crystal structure of cubic \(\beta\)-SiC. Yellow and black spheres mark silicon and carbon atoms, respectively.
The table shown below clearly indicates that earlier experimental data differs considerably from the computed elastic coefficients [3], whereas more recent experiments show very good agreement [7]. This illustrates the difficulties in obtaining reliable measured data. In the present case the discrepancies between the early and more recent data are likely due to the difficulties in synthesizing stoichiometric and defect-free silicon carbide single crystals.
| Expt. [3] | Expt. [7] | Computed | |
|---|---|---|---|
| C11 | 290 | 352 | 385 |
| C12 | 235 | 140 | 139 |
| C44 | 55 | 232 | 239 |
| Bulk | 253 | 211 | 221 |
| Young | 748 | 392 – 694 [8] | 430 |
| Shear | 27.5 | 160 [2] | 183 |
11.3.2. Corundum
The crystal structure of corundum Al2O3with the rhombohedral space group \(R\bar{3}c\) is displayed in Figure 11.3.2.1. This structure has six independent elastic coefficients, namely, C11, C12, C13, C14, C33, and C44, which are all automatically identified by MedeA MT.
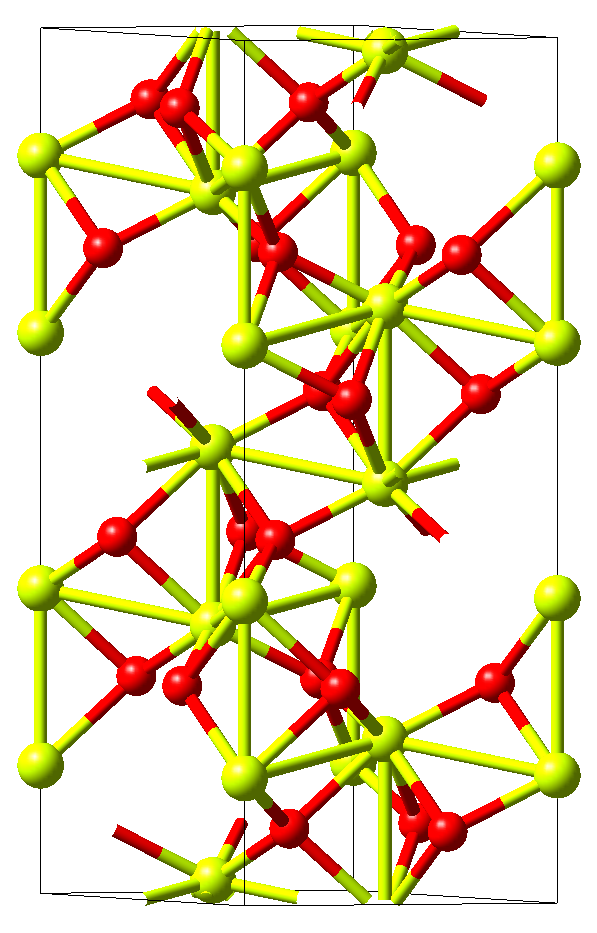
Figure 11.3.2.1 Crystal structure of rhombohedral Al2O3. Yellow and red spheres mark aluminum and oxygen atoms, respectively. The former are octahedrally coordinated by the latter and form long and short metallic bonds parallel to the hexagonal c-axis, which are characteristic also for other corundum-type materials such as Ti2O3\ and V2O3.
Since 1960, literature results on the elastic tensor of corundum, Al2O3were expressed in terms of an unintended reverse setting of the rhombohedral lattice in the hexagonal axes. This led to a change in the sign of the elastic coefficient C14, as reported by Goto et al. [9]. Computations of the elastic coefficients revealed the discrepancy and were confirmed by the newer measurements by Gladden et al. [10], which corrected this inconsistency and at the same time revealed the good agreement of experimental and computed data.
| Expt. [9] | Expt. [10] | Computed | ||
|---|---|---|---|---|
| Sample 1 | Sample 2 | |||
| C11 | 497.3 | 495.6 | 497.4 | 495 |
| C12 | 162.8 | 160.2 | 158.3 | 171 |
| C13 | 116.0 | 117.0 | 121.0 | 130 |
| C14 | -21.9 | +22.1 | +23.0 | +20 |
| C33 | 500.9 | 501.0 | 505.8 | 486 |
| C44 | 146.8 | 147.0 | 145.3 | 148 |
11.3.3. Ferric tourmaline (schörl)
The crystal structure of ferric tourmaline (schörl) NaFe3\ B3\ Al6O30H3\ F with the rhombohedral space group \(R3m\) is displayed in Figure 11.3.3.1.
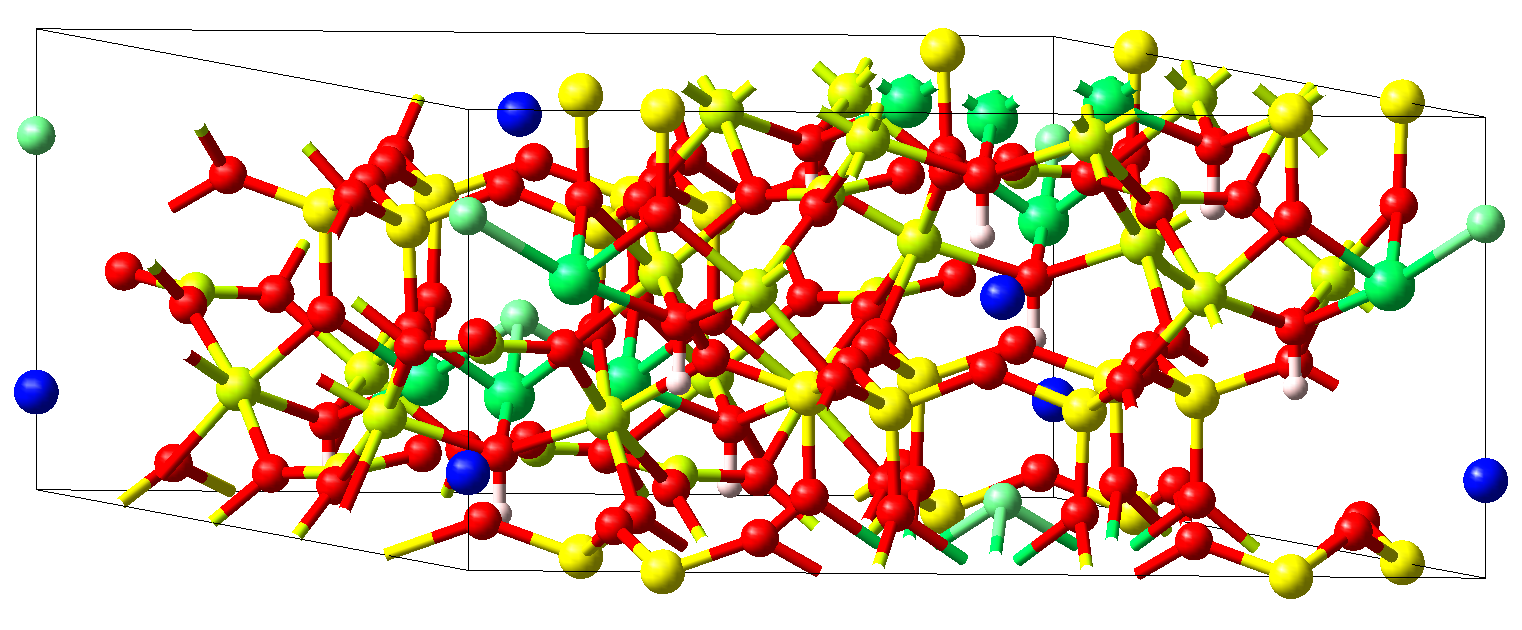
Figure 11.3.3.1 Crystal structure of rhombohedral ferric tourmaline NaFe3\ B3\ Al6O30H3\ F. Fe atoms (green) are found at the centers of edge-sharing octahedra formed from five oxygen atoms (red) and one fluorine atom (light green). These octahedra are arranged in triangular plaquettes alternating with single Na atoms (blue) to form chains along the hexagonal c-axis. Due to the rhombohedral lattice neighboring chains are shifted by one third of this axis and the plaquettes thus form intertwining spirals. The peculiar arrangement of the magnetic ions may give rise to complex magnetic behavior within this class of materials including frustration effects and exciting spin dynamics.
Computations of the six independent elastic coefficients of this rhombohedral structure C11, C12, C13, C14, C33, and C44 can again be routinely applied and reveal even for this rather complex system a good agreement between experimental and computed data.
| Expt. [11] | Computed | |
|---|---|---|
| C11 | 306 | 322 |
| C12 | 109 | 109 |
| C13 | 53 | 56 |
| C14 | -8 | -16 |
| C33 | 174 | 182 |
| C44 | 65 | 62 |
11.4. Conclusion
As demonstrated by the above examples, atomistic computations have emerged as a reliable and independent source for elastic properties, which can be used instead of experimental data with a high level of confidence. In fact, as the example of corundum has shown computations can even identify errors, which have crept into experimental data.
More importantly, the examples discussed in this note illustrate that computed and experimental data are of comparable reliability. However, computed results are obtained much quicker. Furthermore, they allow the study on systems with defects, impurities, and alloying elements where experimental exploration would be very costly and time consuming.
Last but not least, computer simulations open new perspectives in obtaining materials property data. For example, elastic properties can be computed for systems under external strain as it might occur near a crack tip, in a thin corrosion film, or in a nanoscale semiconductor device. Direct measurements of elastic properties under such conditions would be rather difficult if not impossible.
MedeA modules used in this application
- MedeA Environment
- MedeA VASP
- MedeA MT
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | (1, 2) “NSM Archive - Silicon Carbide (SiC) - Mechanical Properties, Elastic Constants, Lattice Vibrations”, in: Electronic archive of “New Semiconductor Materials. Biology systems. Characteristic and Properties”, (Ioffe Physico-Technical Institute, 1998-2001) (DOI) |
| [3] | (1, 2, 3) E. Wiberg, “Gmelins Handbuch der anorganischen Chemie”, (DOI) |
| [4] | Y. Le Page and P. Saxe, “Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress”, Phys. Rev. B 64, 104104 (2002) (DOI) |
| [5] | G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”, Phys. Rev. B 54, 11169 (1996) (DOI); “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set”, Comput. Mater. Sci. 6, 15 (1996) (DOI) |
| [6] | P. E. Blöchl, “Projector augmented-wave method”, Phys. Rev. B 50, 17953 (1994) (DOI) |
| [7] | (1, 2) K. Kunc, M. Balkanski, and M. A. Nusimovici, “Lattice dynamics of several AN B8–N compounds having the zincblende structure. II. Numerical calculations”, phys. stat. sol. (b) 72, 229 (1975) (DOI) |
| [8] | G. L. Harris (ed.), “Properties of Silicon Carbide”, (INSPEC, Institution of Electrical Engineers, 1995). |
| [9] | (1, 2) T. Goto, O. Anderson, I. Ohno, and S. Yamamoto, “Elastic constants of corundum up to 1825 K”, J. Geophys. Res. 94, 7588 (1989) (DOI) |
| [10] | (1, 2) J. R. Gladden, J. D. Maynard, J. H. So, P. Saxe, and Y. Le Page, “Reconciliation of ab initio theory and experimental elastic properties of Al2O3” , Appl. Phys. Lett. 85, 392 (2004) (DOI) |
| [11] | B. G. Helme and P. J. King, “The elastic constants of iron tourmaline (schörl)”, J. Mater. Sci. 13, 1487 (1978) (DOI) |
| Revision: | 7922 |
|---|---|
| download: | pdf |