25. Effect of Resin Molecular Architecture on Epoxy Thermoset Mechanical Properties
The effect of resin molecular architecture on the small strain elastic constants of diamine-cured epoxy thermosets has been studied using classical all-atom simulations conducted within the MedeA ® [1] simulation environment [2]. Batches of thermoset systems have been created using chemically similar di, tri and tetrafunctional resins, followed by calculation of stiffness and compliance matrices for each individual model. Analysis of the batches of topologically and geometrically distinct structures using the Hill-Walpole approach yields upper and lower bounds estimates of the moduli differing by typically 1%, enabling critical comparison with experimentally-measured values.
Keywords: Thermoset, Mechanical Properties, Modulus, Epoxy
25.1. Introduction
Epoxy thermosets, generally formed by reacting a tetrafunctional amine with an epoxide, form a class of polymeric material widely used in advanced composite applications in the aerospace, automotive, electronics and other industries. Their frequent use in composites, in combination with fiber or particulate reinforcing material, leads to a strong research interest in understanding the relationship between the chemical nature and molecular architecture of individual components and characteristics such as mechanical, thermal and adhesive properties, which is required in order to predict accurately the behavior of the final composite material.
The present application note focuses on one particular aspect of epoxy-based matrix material, namely the effect of varying the chemical functionality [3] of the resin component on the small strain elastic constants of the crosslinked resin. Specifically, using the standard nomenclature RAfa+R’Bfb polymerization types applied to such reactions [4], where fa and fb denote the functionality of individual reactants, we concentrate here on comparing the elastic constants of RA4+R’B2, RA4+R’B3 and RA4+R’B4 type systems.
25.2. Materials Studied
In the studies described in this note, the crosslinker RA4 (or curing agent, or hardener) is diaminodiphenylsulfone (DDS) depicted in the form of the 4,4’ isomer in Figure 25.2.1.
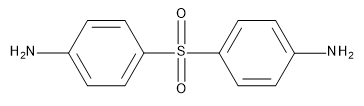
Figure 25.2.1 4,4’-DDS curing agent
The resins used, diglycidyl ether of bisphenol A (DGEBA, R’B2), triglycidyl p-aminophenol (TGAP, R’B3) and tetraglycidyl diaminodiphenylmethane (TGDDM, R’B4) are chemically similar but contain different numbers of glycidyl ether end groups capable of reacting with the amine, as shown in Figure 25.2.2.
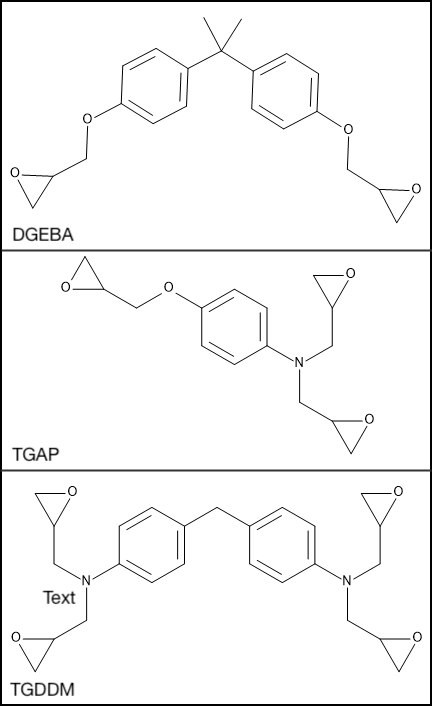
Figure 25.2.2 Di, tri and tetrafunctional resins, (Top) DGEBA, (Middle) TGAP and (Bottom) TGDDM.
25.3. Modeling Details – Crosslinking Reaction
The chemical reaction between a primary amine and the reactive oxirane rings in the resin is illustrated in Figure 25.3.1.:
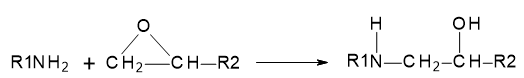
Figure 25.3.1 Reaction between the primary amine and oxirane ring.
A further reaction with the secondary amine group, which is significantly more reactive than the hydroxyl group, can then occur, giving a final product with a tertiary amine structure, i.e.
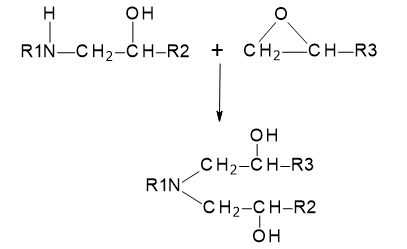
Figure 25.3.2 Subsequent crosslinking reaction involving secondary amine groups.
This implies that in order to obtain 100% reaction of all functional groups when preparing epoxy resins, a ratio of two epoxy groups to one amine moiety is required.
For molecular modeling and simulation purposes it is convenient to work with ‘network segments’, in a manner similar to that used when building models of ordinary polymers where repeat units as opposed to actual monomers are generally used. In the case of the present epoxy-amine reactions, the oxirane rings of the resin are opened as shown in Figure 25.3.3, creating the terminal methyl shown in bold type, such that the crosslinking reaction can be completed by linking the terminal carbon with an amine nitrogen, followed by deletion of hydrogen atoms.
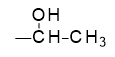
Figure 25.3.3 Network segment epoxy units used in the uncured crosslinkable system.
25.4. Modeling Details – Simulation & Analysis
Since epoxy resins are essentially structurally disordered systems, capable of adopting many topologically distinct structures, computation of average material properties of each individual resin system requires generation of large ensembles of individual configurations, with the details depending on overall system size and the property of interest. In the present work, in which the primary interest is in studying the small strain mechanical behavior, we have chosen to generate batches of 100 independent crosslinked thermoset configurations for subsequent simulation and property calculation, with each system containing between 3000 and 4000 atoms. For studies of tensile and other moduli of amorphous polymer glasses, this procedure has previously been shown to be of sufficiently high precision to predict differences of a fraction of a gigapascal, equivalent to a few percent, in tensile moduli [5].
In order to create the individual systems, we have made use of the MedeA Amorphous Materials Builder to create ‘uncured’ mixture systems, followed by use the MedeA Thermoset Builder, which creates densely crosslinked structures with minimal internal strain using the capture sphere approach pioneered by Eichinger and coworkers [6] [7] for studying the properties of lightly crosslinked polymers, combined with commonly applied minimization and molecular dynamics approaches to effect structural relaxation following crosslink formation. Typically, the procedure results in structures with a range of extents of reaction, as illustrated in Figure 25.4.1, with an average conversion of ~90±1% of the available reactive groups.
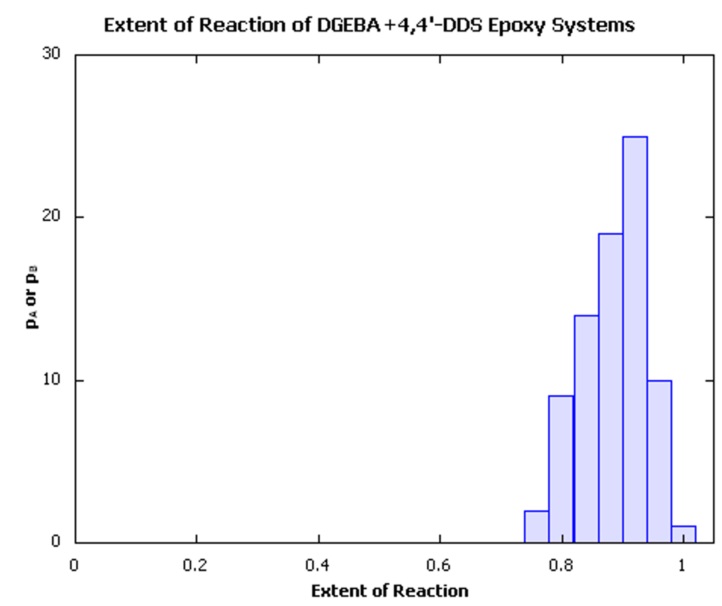
Figure 25.4.1 Distribution of extents of reaction of a batch of crosslinked epoxy thermoset models.
Each crosslinked structure was then subjected to further equilibration using the LAMMPS [8] simulation program in conjunction with the PCFF+ forcefield [9] – an extension of the PCFF (and CFF93) forcefield [10] in which the parameters describing nonbonded interactions have been refined to give accurate predictions of the equation of state properties of organic materials over broad ranges of temperature and pressure. Following equilibration of the density using constant pressure molecular dynamics at 298 K, the 6x6 stiffness and compliance matrices, and associated moduli, were determined by applying six tensile and six shear deformations with minimization following each stage [11], until the maximum force on any atom falls below 1.0 x 10-6 kcal mol-1 Å-1.
To avoid the significant manual effort involved in repetitively building uncured systems, crosslinking, performing atomistic simulations and analyzing the resulting structures to obtain predictions of mechanical properties, the entire procedure has been encapsulated in a single flowchart created within the MedeA interactive environment, with job submission and data processing managed by the MedeA Jobserver/Taskserver browser-controlled architecture. Building, simulation and analysis of a typical batch of 50 thermoset structures requires approximately 2 days on a small cluster using say 12-24 cpu cores.
25.5. Results and Discussion
As is invariably the case with mechanical property calculations on amorphous glasses, a distribution of individual elastic constants is obtained depending on the detailed local packing, as illustrated in Figure 25.5.1 below, which depicts the distribution of individual moduli obtained from the stiffness matrix of each sample.
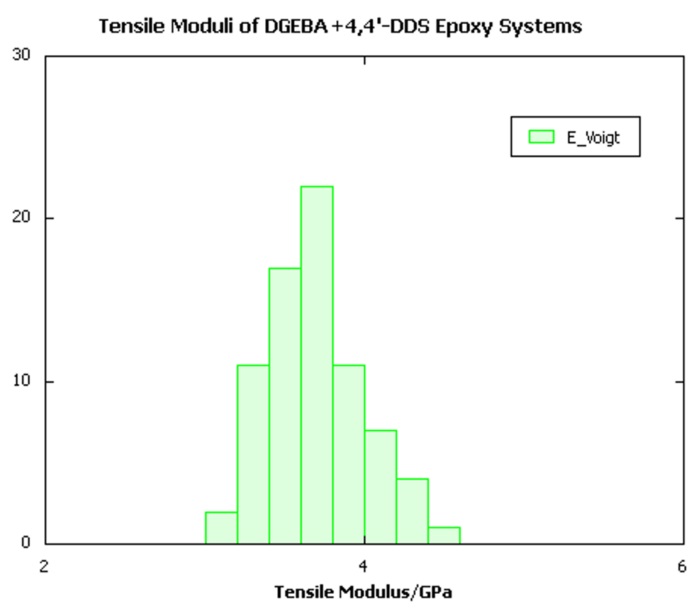
Figure 25.5.1 Distribution of tensile moduli extracted from stiffness matrices of a batch of DGEBA/4,4’-DDS crosslinked systems.
From the literature on composite materials, it is well known that estimates of the upper and lower bounds of the moduli – the so-called Voigt and Reuss bounds – can be obtained from averages of the stiffness and compliance matrices respectively. However, as pointed out by Suter and Eichinger [12], when this approach is applied to obtain modulus estimates for atomistic-scale models with linear dimensions of a few tens of Angstroms, the differences in upper and lower bounds are too large to be of practical use for distinguishing between the mechanical properties of all but the most dissimilar materials. Accordingly, these workers applied a more sophisticated approach, based on the early work of Hill [13] and Walpole [14] , to compute more rigorous and precise bounds estimates of the moduli obtained using atomistic scale models. They then proceeded to demonstrate that the method is effective for analyzing glassy polystyrene data, which has since been shown in this laboratory to be successfully applicable to other glassy systems [2].
The Hill-Walpole based bounds estimates obtained in this manner for the crosslinked epoxy systems studied in this work are presented in Table 1 below, in which the predicted modulus bounds for the three resin architectures are compared with available experimental data.
| Resin | Calculated Bounds (GPa) | Experiment (GPa) |
|---|---|---|
| DGEBA | 3.49-3.53 | 2.4-3.2a |
| TGAP | 4.42-4.45 | 4.396 \(\pm\) 0.027b |
| TGDDM | 5.18-5.19 | 5.103 \(\pm\) 0.033c |
a. Extents of reaction 0.5-1.0; ~300K; using dynamic mechanical analysis at 1Hz [15].
b. Extent of reaction 0.93; 295K; strain rate 1.67 x10-2s-1 [16].
c. Extent of reaction 0.88; 295K; strain rate 1.67 x10-2 s-1 [16].
Before comparing the experimentally-measured and simulation-derived data, it is worthwhile noting that in the case of the three and four functional TGAP and TGDDM resin based epoxies, the experimental data exhibit an increase in modulus with increasing strain rates in the compressive stress-strain experiments used for the measurements. Since the method used to obtain moduli in the simulations effectively corresponds to a very high strain rate involving instantaneous initial deformations, we have therefore chosen to perform comparisons with the experimental data at the highest strain rates, which are least affected by viscoelastic effects. In the case of the difunctional DGEBA based epoxies, no information other than the frequency of measurement is available and, moreover the actual strain rate is unknown.
Focusing on the tensile moduli calculated for all three resin architectures, it is clear that the Hill-Walpole analysis indeed yields well-defined ranges of moduli for each system, each of which is considerably narrower than the typical width of the range of individual elastic constants illustrated in Figure 25.5.1. Moreover, comparison with the experimental data shows remarkably good agreement with the high strain rate measurements for the trifunctional and tetrafunctional TGAP and TGDDM systems. For the DGEBA system, the calculated tensile modulus of around 3.5GPa appears to be slightly higher than the upper experimental bound of around 3.2GPa. The precise origin of the discrepancy, which although small may be statistically significant, remains unclear. However, factors such as uncertainty in the experimental degree of conversion, strain rate effects, and the exact chemical composition of the resin, which in commercial samples may contain molecules with more than one bisphenol A group per molecule, may warrant further investigation.
In conclusion, it appears that strain free all-atom models of densely crosslinked thermosets can be created with cure states comparable with experiment. Calculation of elastic moduli, with appropriate averaging of moderately large batches of structures, yield precise bounds estimates in good agreement with available experimental data.
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | (1, 2) D. Rigby, P.W. Saxe, C.M. Freeman and B. Leblanc, “Computational Prediction of Mechanical Properties of Glassy Polymer Blends and Thermosets”, in Advanced Composites for Aerospace, Marine and Land Applications, T. Sano, T.S. Srivatsan and M.W. Paretti (Eds), 157-172, John Wiley (2014)] (DOI) |
| [3] | Chemical functionality denotes the maximum number of chemical reactions each component of a crosslinkable material is capable of undergoing |
| [4] | P.J. Flory, “Principles of Polymer Chemistry”, Cornell Univ. Press, Ithaca, New York (1953), Ch. 9 |
| [5] | P.W. Saxe, C.M. Freeman and D. Rigby, AIChE Annual Meeting, 2012 |
| [6] | B. E. Eichinger and Ö. Akgiray, “Computer Simulation of the Formation of Polymer Networks”, Makromolekulare Chemie. Macromolecular Symposia 76, 211 (1993) (DOI) |
| [7] | L.Y. Shy, Y.K. Leung and B.E. Eichinger, “Critical Exponents for Off-Lattice Gelation of Polymer Chains” Macromolecules 18, 983 (1985) (DOI) |
| [8] | S.J. Plimpton, “Fast Parallel Algorithms for Short-Range Molecular Dynamics”, J. Comput. Phys., 117, 1 (1995) (DOI) |
| [9] | D. Rigby, to be published (2020) |
| [10] | see, for example, H. Sun, S.J. Mumby, J.R. Maple and A.T. Hagler, “An ab initio CFF93 All-Atom Force Field for Polycarbonates”, J. Am. Chem. Soc. 116, 2978 (1994) (DOI) |
| [11] | D.N. Theodorou and U.W. Suter, “Atomistic Modeling of Mechanical Properties of Polymeric Glasses”, Macromolecules 19, 139 (1986) (DOI) |
| [12] | U.W. Suter and B.E. Eichinger, “Estimating Elastic Constants By Averaging Over Simulated Structures,” Polymer 43, 575 (2002) (DOI) |
| [13] | R. Hill, “A Self-Consistent Mechanics of Composite Materials”, J. Mech. Phys. Solids 13, 213 (1965) (DOI) |
| [14] | L.J. Walpole, “On Bounds for the Overall Elastic Moduli of Inhomogeneous Systems-I”, J. Mech. Phys. Solids 14, 151 (1966) (DOI) |
| [15] | S.R. White, P.J. Mather and M.J. Smith, “Characterization of the Cure State of DGEBA-DDS Epoxy Using Ultrasonic, Dynamic Mechanical and Thermal Probes”, Polym. Eng. Sci. 42, 51 (2002) (DOI) |
| [16] | (1, 2) S. Behzadi and F.R. Jones, “Yielding Behaviour of Model Epoxy Matrices for Fiber-Reinforced Composites: Effect of Strain Rate and Temperature”, J. Macromol. Sci. Part B:Phys., 44, 993 (2005) (DOI) |
Modules Used in This Application
- MedeA Environment including Flowcharts and MedeA LAMMPS user interface
- MedeA Amorphous Materials Builder and MedeA Thermoset Builder
- MedeA MT mechanical properties module
| download: | pdf |
|---|