35. Automating High Accuracy Gaussian Calculations with MedeA Flowcharts
Keywords: GAUSSIAN, High-Precision, High-Throughput, Chemical accuracy
35.1. Introduction
Assessing the accuracy of a computational approach is one of the most difficult tasks in materials modeling. By accuracy we mean here the level of agreement with physical experiments. MedeA can help you in this important task with its comprehensive range of different computational tools and very convenient high-throughput computational workflows. The present application note shows this for the case of subtle interatomic interactions, which often determine properties such as the density of molecular crystals and the vapor pressure of fluids. Specifically, this is illustrated for dimers of rare gas atoms.
The purpose of this application note is also to illustrate the use of Gaussian in the calculation of interaction energies. In addition, the utility of the MedeA High-Throughput Launchpad module in automating calculations is illustrated.
The quantum chemical coupled cluster method with singlet (S), doublet (D) and triplet (T) excitations (CCSD(T)) is the gold standard of quantum chemists [1]. It calculates energies and forces with high accuracy [2] [3]. CCSD(T) explicitly takes into account the electronic exchange and correlation contributions and can thus describe effects such as subtle van der Waals attraction.
Here, we demonstrate the ability of CCSD(T) to accurately predict the potential energy surface of rare gas dimers, namely, He, Ne, and Ar. Rare gas dimers are experimentally well characterized [2]. Rare gases are also industrially critical and relevant: they are formed in fission and fusion reactors and in actinide decay, leading to material damage (swelling and fragmentation of nuclear fuel and embrittlement of structural materials of nuclear plants) [4] [5] [6].
In this application note, MedeA and Gaussian are used to build the models and calculate the energies and forces using standardized flowcharts [7]. The results are discussed and compared with experimental reference data. The CCSD(T) results are in excellent agreement with the experimental values.
35.2. Methods and Models
The atomistic models are constructed using the building tools of MedeA. Among the stages accessible in the MedeA flowcharts, the Structure List stages (New List, Save to List, etc.) are used to create the structures, perform the energy calculations, and save and tabulate the results. The Translate Atoms stage is used to build the He-He, Ne-Ne, and Ar-Ar dimers at different distances under periodic conditions, and the structures are stored in MedeA structure lists. About 30 pair structures are built with an incremental distance of 0.1 Ang between the atoms for each He-He, Ne-Ne, and Ar-Ar pair. Energy calculations are performed using Gaussian [8] under non-periodic conditions. The Gaussian stage is used for the energy calculations. The tasks on the structure lists are performed using the For Each Structure stage in the same flowchart for a given dimer (Figure 35.2.1). More details about flowcharts and stages can be found in the MedeA tutorials repository (https://www.materialsdesign.com/tutorials).
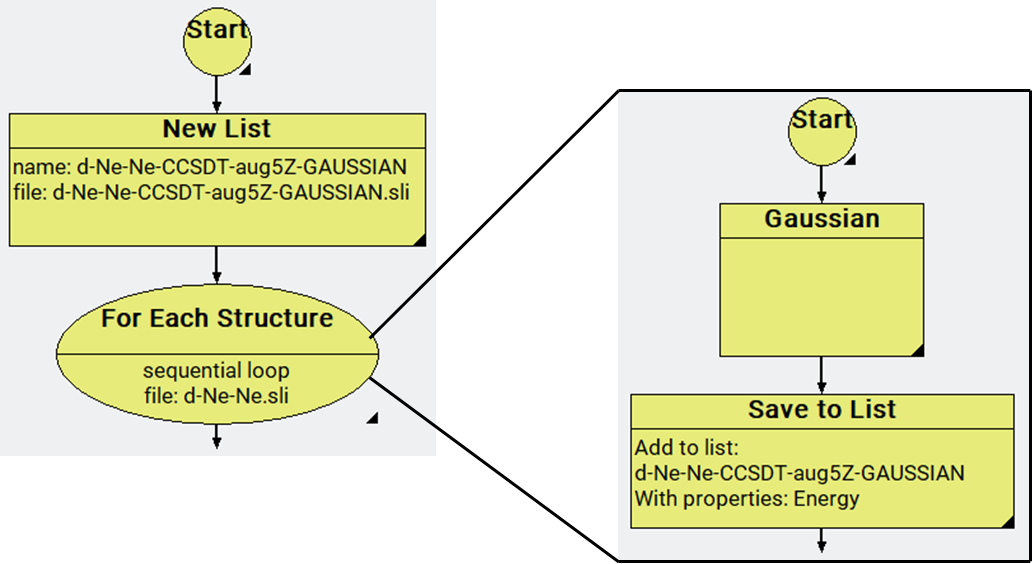
Figure 35.2.1 The MedeA flowchart for Ne-Ne profile.
The flowchart is executed by the MedeA JobServer. The MedeA JobServer additionally carries out job management and distribution and stores all the information for a given job, allowing easy access and sharing of calculation results. An image of the JobServer is show in Figure 35.2.2.
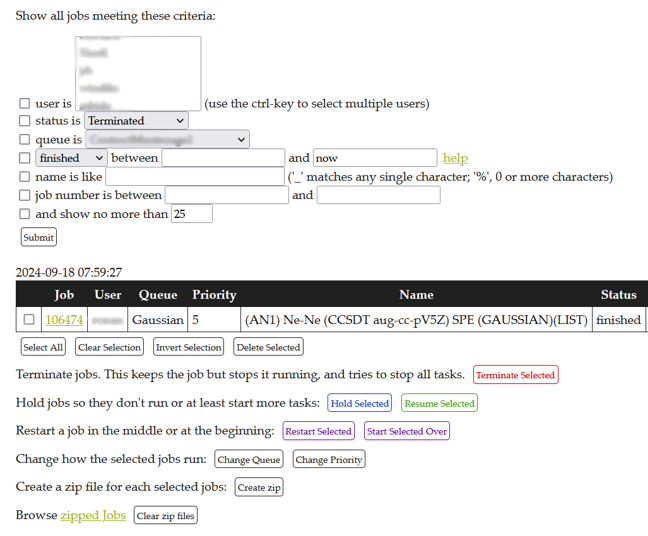
Figure 35.2.2 The MedeA JobServer with the information about the Ne-Ne Job.
CCSD(T) uses localized basis sets. Due to the mathematical incompleteness of the basis set and the inherently slow energy convergence of the post-Hartree Fock methods with the basis set size, CCSD(T) suffers from basis set superposition error (BSSE) [2] [3] [9] [10]. Therefore, an analysis of the energy profiles of Ar-Ar with different basis sets has been performed to analyze the convergence of the results with increasingly large basis sets (Figure 35.2.3).
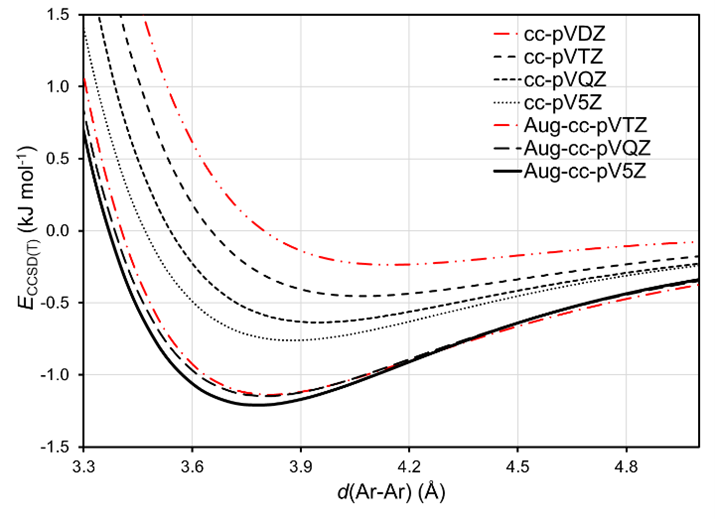
Figure 35.2.3 CCSD(T) energy profiles of Ar-Ar with different basis sets.
From the Figure, it appears that the energy profile converges well with the Aug-cc-pV5Z basis set, which was used in all subsequent calculations. Moreover, the tails of the curves show the expected Van der Waals r-6 behavior. Since the computational time and memory of CCSD(T) scale as n7, where n is the number of valence electrons in the system, it is not always possible to use large basis sets for large molecular systems. Also, not all basis sets are available for all elements in the periodic table. The Gaussian stage Configure basis and pseudopotentials provides a clear overview of the basis sets availability.
The available experimental data for the He-He, Ne-Ne, and Ar-Ar pairs are the distance (\(r_{0}\)) and energy well depth (\(E_{min}\)) of the minimum in the energy profile. To obtain the best accuracy on the values of \(r_{0}\) and \(E_{min}\), an analytical mathematical function is used and fitted on the calculated energies around the minimum.
35.3. Results
The experimental and calculated positions of the minima for the He-He, Ne-Ne, and Ar-Ar pairs are given in Table 1.
Table 1: Experimental and calculated distances and well depths of the minima in the He-He, Ne-Ne, and Ar-Ar pairs.a
| Pair | \(r_{0}\) | \(E_{min}\) | ||
|---|---|---|---|---|
| Exp. | CCSD(T) | Exp. | CCSD(T) | |
| He | 2.97 | 3.00 | -0.09 | -0.09 |
| Ne | 3.09 | 3.11 | -0.35 | -0.36 |
| Ar | 3.76 | 3.77 | -1.19 | -1.21 |
a\(r_{0}\) is in Ang. \(E_{min}\) is in kJ mol-1. The experimental data are taken from [2]. The basis set for the CCSD(T) calculations is Aug-cc-pV5Z.
The experimental and calculated dimer binding distances and energies for He-He, Ne-Ne, and Ar-Ar are in excellent agreement. The root-mean-square deviations (RMSD) between the experimental and calculated distances and energies are 0.03 Ang and 0.01 kJ mol-1 for the reported values, respectively. The RMSD on \(E_{min}\) is two orders of magnitude smaller than the chemical accuracy, which has a commonly accepted value of 4 kJ mol-1 [1].
35.4. Conclusions and Perspectives
This application note illustrates (i) how easy it is to manage calculations with MedeA, (ii) the accuracy of the methods available in Gaussian, and (iii) the power of a flowchart environment to automate and standardize the protocol of calculations.
The calculation methods available in MedeA cover many atomistic simulation methods. They range from the highly accurate electronic post-Hartree-Fock methods, which include explicit electronic exchange and correlation contribution, to empirical correlation methods. CCSD(T) is shown to be highly accurate compared to experimental data. Such an approach, although computationally demanding, can be used to establish the gold standard reference for a given system and to validate the accuracy of more approximate atomistic simulation methods when experimental values are not available.
The MedeA flowchart environment is very powerful for automating and standardizing simulation protocols. Once the simulation flowcharts were created, the human intervention was minimal, minimizing the risk of human error. A flowchart can be used on a wide range of systems with little to no modification, hence establishing standardized, reusable protocols. This application note focuses on isolated rare gas dimers. Similar simulation protocols can be applied to any atomic system using the MedeA materials modeling environment to explore the origin of any desired physical material property.
| [1] | (1, 2) M. Bursch, J. Mewes, A. Hansen, and S. Grimme, “Best-Practice DFT Protocols for Basic Molecular Computational Chemistry.” Angew. Chem. Int. Ed. 61:e202205735 (2022) (DOI). |
| [2] | (1, 2, 3, 4) S. M. Cybulski, and R. R. Toczylowski, “Ground State Potential Energy Curves for He2, Ne2, Ar2, He-Ne, He-Ar, and Ne-Ar: A Coupled-Cluster Study.” J. Chem. Phys. 111: 10520-10528 (1999). (DOI). |
| [3] | (1, 2) D. Feller, K. A. Peterson, and J. Grant Hill, “On the Effectiveness of CCSD(T) Complete Basis Set Extrapolations for Atomization Energies.” J. Chem. Phys. 135: 044102 (2011) (DOI). |
| [4] | G. W. Egeland, J. A. Valdez, S. A. Maloy, K. J. McClellan, K. E. Sickafus, and G. M. Bond, “Heavy-Ion Irradiation Defect Accumulation in ZrN Characterized by TEM, GIXRD, Nanoindentation, and Helium Desorption.” J. Nucl. Mater. 435: 77-87 (2013) (DOI). |
| [5] | A. van Veen, R. J. M. Konings, and A. V. Fedorov, “Helium in Inert Matrix Dispersion Fuels.” J. Nucl. Mater. 320: 77-84 (2003) (DOI). |
| [6] | Hj. Matzke, “Radiation Damage in Nuclear Fuel Materials”. SSP 30-31: 355-366 (1992) (DOI). |
| [7] | Materials Design, MedeA 3.6 (Materials Exploration and Design Analysis) (2024). www.materialsdesign.com. |
| [8] | M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, ; G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16 Rev. C.01 (2016). |
| [9] | J. A. Sordo, S. Chin, and T. L. Sordo, “On the Counterpoise Correction for the Basis Set Superposition Error in Large Systems”. Theo. Chim. Acta 74: 101-110 (1988) (DOI). |
| [10] | E. R. Davidson, and S. J. Chakravorty, “A Possible Definition of Basis Set Superposition Error.” Chem. Phys. Lett. 217: 48-54 (1994) (DOI). |
| download: | pdf |
|---|