6. Properties of natural gases in classical and in HP-HT conditions
In this note, we illustrate the predictive power of MedeA®[1] in describing the influence of pressure, temperature and composition on natural gas behavior, up to the conditions of HP-HT gases.
Keywords: natural gas, HP-HT conditions, ideal heat capacity, Joule Thomson coefficient, compressibility, speed of sound
6.1. Introduction
Typical High Pressure - High Temperature (HP-HT) conditions may be defined by fluid pressures in excess of 50 MPa or temperatures above 150°C, as encountered in deep reservoirs below the North Sea, the Caspian Sea, the Gulf of Mexico and offshore Brazil, among others. Under these conditions natural gas may contain hydrocarbons with chain length of as much as 30 carbon atoms and a methane content higher than 60% (molar concentration) [2]. Because of the high temperature, water content may be significant, and further, H2S or CO2contents may be elevated in some HP-HT reservoirs.
Under these conditions, the use of standard equations of state to compute volumetric properties becomes questionable. Nevertheless precise knowledge of volumetric properties is desirable for the following reasons:
- The amount of gases and liquids that can be produced by primary recovery directly depends on the volumetric properties.
- During production, these fluids are known to heat up in an adiabatic expansion; this should be considered when selecting well equipment [3].
PVT measurements under high pressure require heavy instruments, with long delays and high costs as a consequence. Also, the small volume of gas sample available makes direct measurements very difficult for some properties (e.g. Joule-Thomson coefficient).
From today’s perspective, recent advances in computational power, molecular simulation methodologies and graphical user interfaces have rendered complex mixtures accessible for molecular simulations, provided their composition is known from analysis [4].
Also in favor of molecular modeling speaks the fact that computational parameters developed by validating against well-known pure compounds [5] are transferable to heavier hydrocarbons.
6.2. Methods
In order to obtain the thermodynamic properties of ideal gases at any desired temperature, we used the quantum molecular software MOPAC with the semi-empirical potential PM7 [6].
Simulating fluid mixtures at high pressure is done using Monte Carlo sampling as available in the MedeA GIBBS software (single phase simulation in the isobaric-isothermal NPT ensemble). Combining this approach with molecular quantum mechanics allows to obtain thermodynamic properties like the Joule-Thomson coefficient [5] or the speed of sound for mixtures, in non-ideal conditions. In applying this method we have used the AUA forcefield for hydrocarbons, similarly to previous work [3].
6.3. Results
Simple pure fluids like ethane are very well described as can be seen in (Figure 6.3.1).
For a more complex natural gas mixture [8] in the modest pressure range of 20-30 MPa (Figure 6.3.2), the influence of temperature and pressure on the compressibility factor Z (Z=PV/RT) is well captured.
Here, the reason of the systematic difference between observed and predicted compressibility factor is likely to stem from the uncertainty of composition as given in (Table 1).
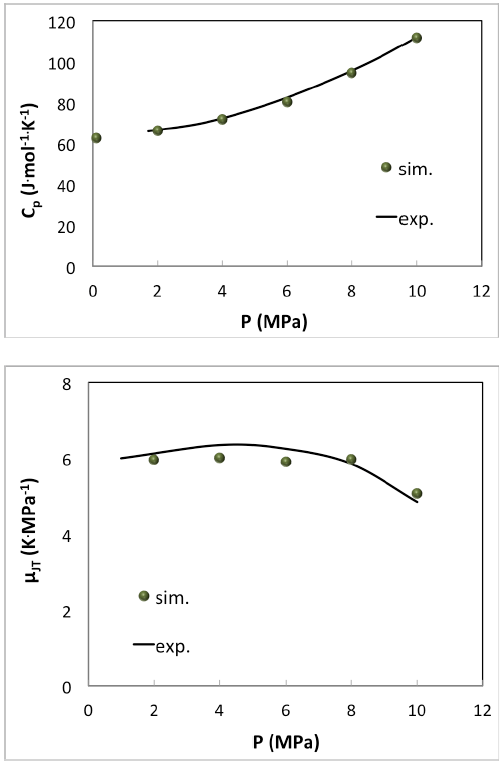
Figure 6.3.1 Simulation of molar heat capacity Cp(top) and the Joule-Thomson coefficient (bottom) of ethane at 377.5 K with MedeA GIBBS compared with experimental measurements [7].
A third example is a HP-HT gas (Figure 6.3.3) already investigated by molecular modeling. In agreement with previous investigations, our computations predict the correct density curve (Figure 6.3.4) and the correct inversion pressure of the Joule-Thomson effect (Figure 6.4.1). In this example, direct measurements of the Joule-Thomson coefficient were not possible, and solely the inversion pressure (42 MPa) at the reservoir temperature (463 K) could be measured [2]. From (Figure 6.4.1) it appears that upon increasing pressure the Joule-Thomson coefficient reaches an asymptotic minimum at approximately -0.4 K/MPa.
| Compound | Nb of molecules | mol % |
|---|---|---|
| CO2 | 1 | 0.2 |
| methane | 408 | 81.6 |
| ethane | 24 | 4.8 |
| propane | 23 | 4.6 |
| 2-methyl-propane | 6 | 1.2 |
| n-butane | 9 | 1.8 |
| 2-methyl-butane | 5 | 1 |
| n-pentane | 4 | 0.8 |
| n-hexane | 9 | 1.8 |
| n-heptane | 3 | 0.6 |
| n-octane | 5 | 1 |
| n-nonane | 3 | 0.6 |
| Total | 500 | 100 |
Other properties of industrial interest can be derived from MedeA GIBBS like the sound velocity of the fluid (Figure 6.4.2).
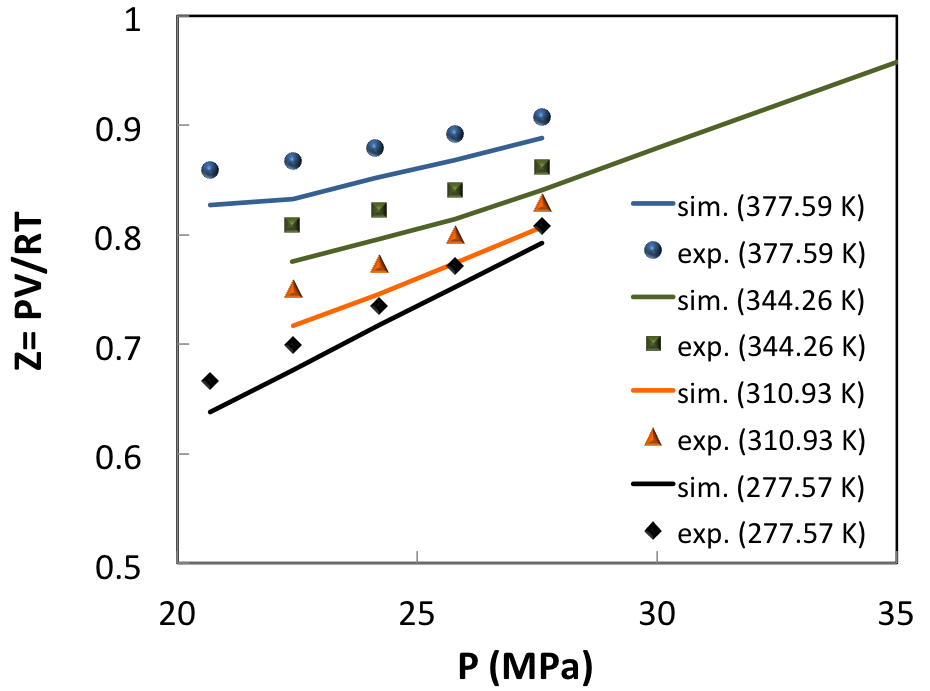
Figure 6.3.2 Compressibility factor of a real condensate gas (system C of ref. [8], see (Table 1)) compared with MedeA GIBBS simulations.
It can be seen that the speed of sound of the natural gas increases significantly with pressure.
This may have consequences in the interpretation of seismic data, because the sound velocity in fluids influences the propagation of acoustic waves in sediments.
Due to this effect, the gas-saturated reservoir in high-pressure conditions (100 MPa) is less likely to display a sharp decrease of seismic velocity as it does in low-pressure conditions.
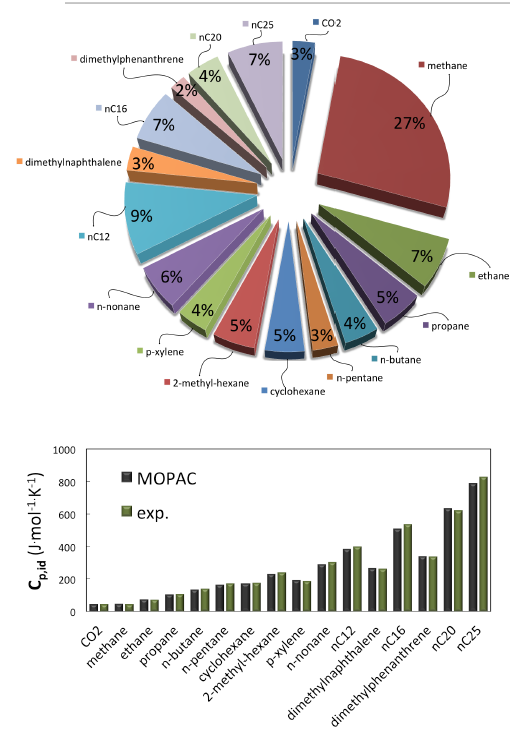
Figure 6.3.3 Top: Composition (mass fraction) assumed for MedeA GIBBS simulations of the HP-HT natural gas (adapted from [3] with minor simplifications); Bottom: Prediction of ideal heat capacity Cp,idat 463 K by quantum mechanics and vibrational analysis (MOPAC-PM7) for each component at 463 K, and comparison with reference data (DIPPR, NIST, IUPAC) at the same temperature. AAD vs reference data is 2.8%.
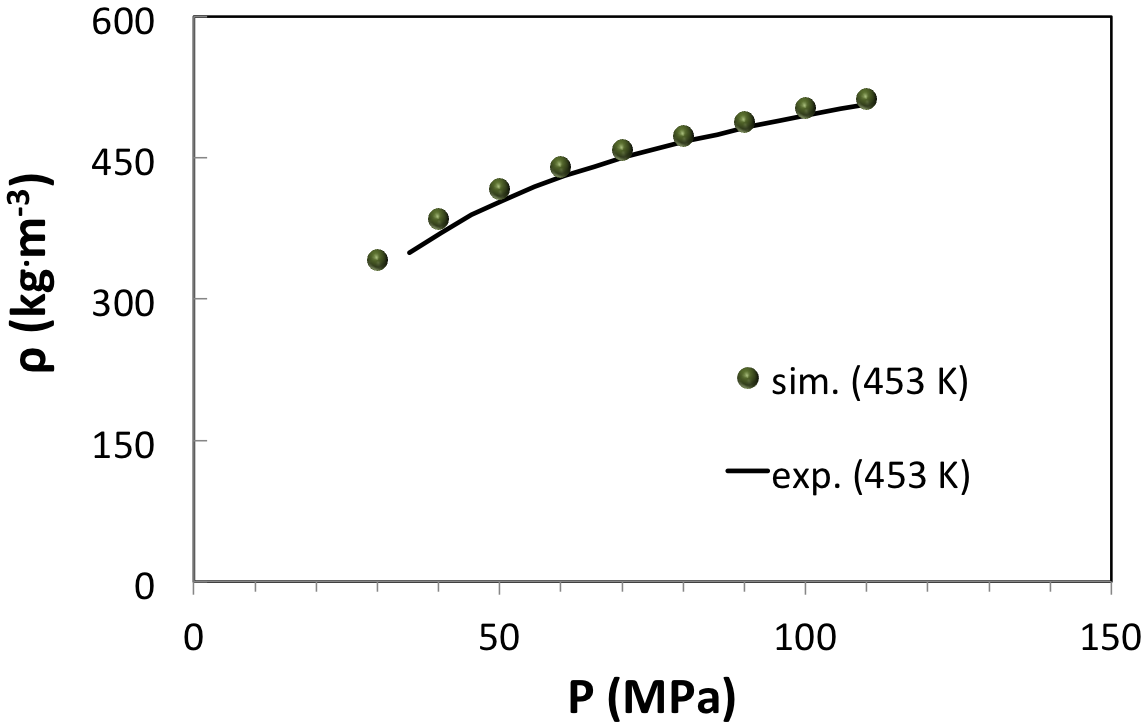
Figure 6.3.4 Density of a HP-HT natural gas from experiments (system B of [2]) and from MedeA GIBBS simulations at 453 K.
6.4. Conclusions – Perspectives
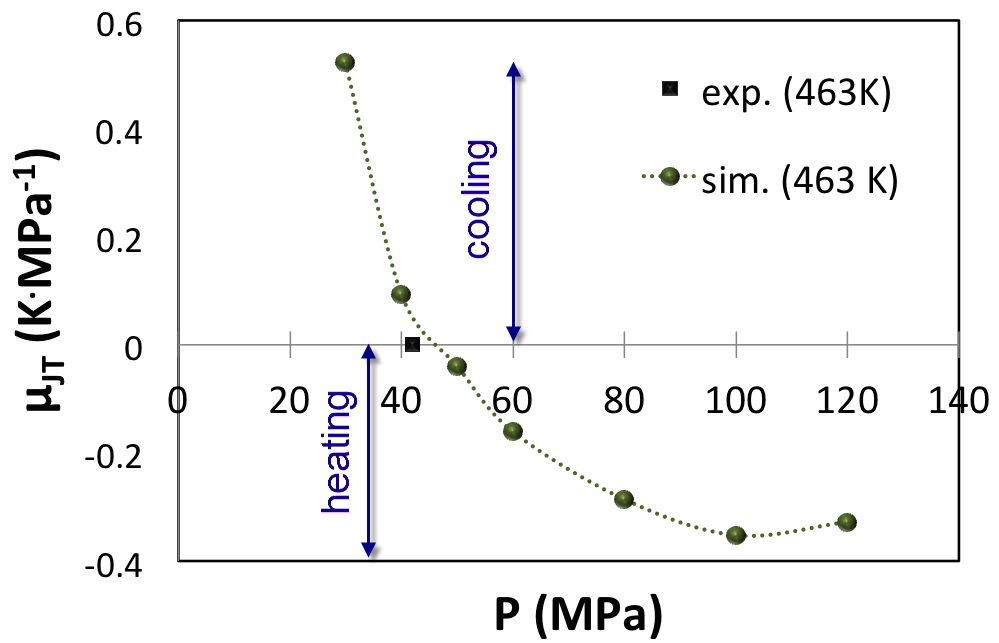
Figure 6.4.1 Joule-Thomson coefficient of HP-HT natural gas from MedeA GIBBS simulations at 463 K. The black square is the inversion temperature determined from experiments at 463 K after Lagache et al. [3].
Starting just from the composition of a given fluid, MedeA GIBBS accurately predicts its thermodynamic properties. The success of the method is founded on efficient statistical mechanics and comprehensive libraries of forcefield parameters building on both experimental data and high precision molecular quantum mechanics.
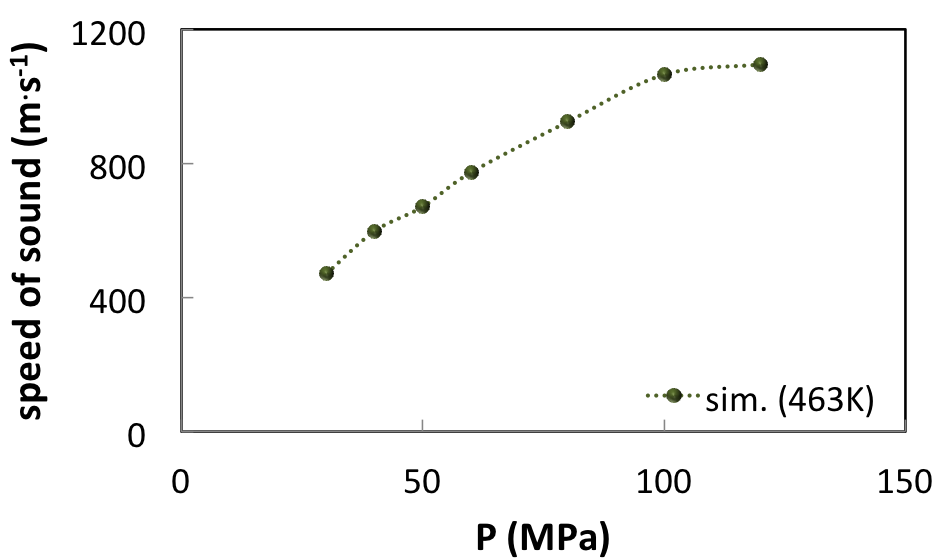
Figure 6.4.2 Speed of sound of the HP-HT reservoir fluid determined from the molar volume and from the isentropic compressibility at 463 K.
In addition, molecular simulations are less limited than equations of state when introducing polycyclic aromatic fractions, for which few experimental measurements are available. As these fractions contribute significantly to increasing the liquid density, accounting for their presence in the model composition allows for more precise calculation of volumetric properties.
Required Modules
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | (1, 2, 3) P. Ungerer, B. Faissat, C. Leibovici, H. Zhou, E. Behar, G. Moracchini, J.P. Courcy, “High pressure-high temperature reservoir fluids: investigation of synthetic condensate gases containing a solid hydrocarbon”, Fluid Phase Equilibria 111, 287 (1995) DOI |
| [3] | (1, 2, 3, 4) M. Lagache, P. Ungerer and A. Boutin, “Prediction of thermodynamic derivative properties of natural condensate gases at high pressure by Monte Carlo simulation”, Fluid Phase Equilibria 220, 211 (2004) DOI |
| [4] | T. Dutriez, M. Courtiade, D. Thiébaut, H. Dulot, F. Bertoncini, and M. C. Hennion, “Extended characterization of a vacuum gas oil by offline LC-high-temperature comprehensive two-dimensional gas”, J. Sep. Sci. 33, 1787 (2010) DOI |
| [5] | (1, 2) M. Lagache, P. Ungerer, A. Boutin, A. H. Fuchs, “Prediction of thermodynamic derivative properties of fluids by Monte Carlo simulation “, Phys. Chem. Chem. Phys. 3, 4333 (2001) DOI |
| [6] | J. P. Stewart, “Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters”, J. Mol. Model. 19, 1 (2013) DOI |
| [7] | K. Bier, J. Kunze and G. Maurer, “Thermodynamic properties of ethane from calorimetric measurements”, J. Chem. Thermodynamics 8, 857 (1976) DOI |
| [8] | (1, 2, 3) B. H. Sage, and R. H. Olds, “Volumetric Behavior of Oil and Gas from Several San Joaquin Valley Fields “, Trans. AIME 170, 156 (1947) DOI |
| download: | pdf |
|---|