20. Thermoelectric Properties of Bi2Te3as calculated using MedeA Electronics
The thermoelectric properties of the prototype material Bi2Te3 are calculated using density functional theory and modern approaches to transport properties as implemented in MedeA Electronics. Complementing a wide portfolio of materials properties accessible from the MedeA computational environment, these calculations establish good agreement with experimental data and thereby underline the predictive power of atomistic simulation of electronic transport. In view of the strong dependence of the transport properties on synthesis conditions the first principles approach recommends itself as a valuable complement of laborious measurements.
Keywords: Thermoelectric properties, Thermopower, Seebeck coefficient, Boltzmann transport theory, Bi2Te3, VASP
20.1. Background
Strong interest in an environmentally friendly use of energy has recently stirred up a large amount of research on thermoelectric materials. As is well known, by means of the Seebeck effect such materials are able to convert (waste) heat into electricity. An appealing aspect of this process is that the energy conversion can be achieved without any moving mechanical parts and that it can be applied even on the nanoscale, i.e. in electronic devices. Thermoelectricity thus offers an elegant route to sustainable energy production and consumption. As such it represents a valuable contribution to the energy supply of the future. Yet, thermoelectricity furthermore allows for exciting applications in sensor technology. While the Seebeck effect is known for almost two centuries its use for energy conversion on a larger scale has been triggered only recently by the advent of modern materials science, which allows to tailor materials on the nanoscale. Several materials (classes) have been identified including mixed semiconductors such as SixGey, layered materials such as NaxCoO2 and delafossite-type materials, scutterudites with their three-dimensional structures including holes, and Bi2Te3, which nowadays is regarded as a prototype material for thermoelectric energy conversion. On the theoretical side, semi-classical Boltzmann transport theory in conjunction with ab initio calculations as based on density functional theory has established as state-of-the-art approach [1], [2], [3], [4], [5]. Using the example of Bi2Te3, this application note demonstrates the capability of atomistic simulations as enabled by the MedeA software environment to access the transport properties of materials and thereby to open design strategies for new thermoelectrics.
20.2. Method of Calculation
Boltzmann transport theory is a semiclassical theory, which relies on the quantum-mechanical calculation of the electronic states but assumes the electrons to follow classical equations of motion between scattering events separated by the so-called relaxation time. At the bottom line, this theory allows to evaluate the Onsager transport coefficients, which relate particle and heat currents to an electric field and a temperature gradient. These coefficients are directly connected to the electric and thermal conductivity as well as the thermopower, which are then deduced from the details of the electronic band structure, i.e. from the electronic states and band velocities. Within the MedeA computational environment this information is obtained using MedeA VASP [6]. Specifically, the electronic states and the band velocities as arising from the electronic band structure are combined into the so-called transport distribution, which eventually leads to the Onsager coefficients. Note that the Onsager coefficients are obtained from energy integration with the energy derivative of the Fermi function in the integrand. As a consequence, they become vanishingly small for semiconductors unless the band gap is very small. Note also that within Boltzmann transport theory the Onsager coefficients depend on the so-called relaxation time. Yet, the thermoelectric power arises as the ratio of two such coefficients and, hence, the relaxation time cancels from the final result to a good approximation.
20.3. Computed Results
Bi2Te3 is a narrow gap semiconductor with the layered trigonal crystal structure shown in Figure 20.3.1. It consists of the periodic arrangement of five-layer sequences, where each layer is made of only one species of atoms. While single Bi layers are throughout sandwiched between Te layers, the tellurium atoms form alternating single and double layers.
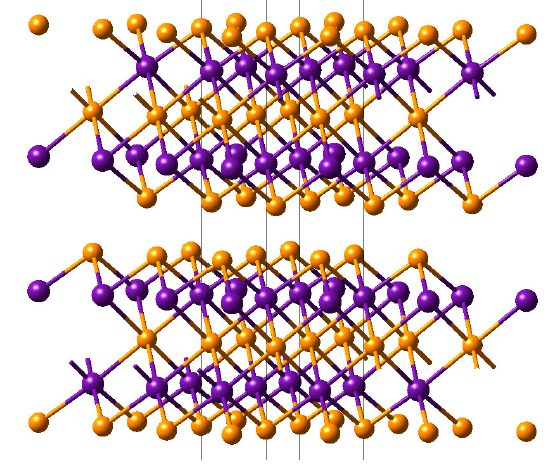
Figure 20.3.1 Crystal structure of Bi2Te3. Bismuth and tellurium atoms are shown in pink and orange, respectively.
The calculated electronic structure as displayed in Figure 20.3.2 reveals an indirect optical band gap of 0.16 eV, which is in very good agreement with the experimental value of 0.18 eV [7]. Worth mentioning are the rather flat bands right below and above the band gap, which lay ground for the high thermoelectric power. The calculations were performed using MedeA VASP [6] including spin-orbit coupling.
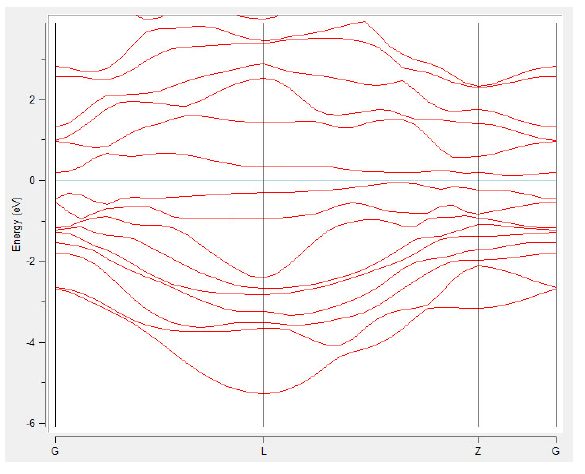
Figure 20.3.2 Electronic band structure of Bi2Te3 along selected lines within the 1st Brillouin zone.
The calculation of the electronic band structure was complemented with the determination of the transport properties as arising from Boltzmann transport theory. To this end, accurately determined electronic states were combined with the standard formulas for the transport distribution as coded in the BoltzTraP code and implemented in MedeA Electronics [8]. The transport distribution was subsequently used to calculate the thermoelectric power. The results are displayed in Figure 20.3.3 and Figure 20.3.4.
In general, the Seebeck coefficient is obtained as a function of temperature. In addition, it is possible to simulate doping within the so-called rigid band shift. We recall that the Onsager coefficients become vanishingly small for semiconductors. Within MedeA Electronics this is taken care of by allowing for an artificial shift of the chemical potential. The result is seen in Figure 20.3.3, where the thermopower is displayed as a function of this chemical potential shift for various temperatures.
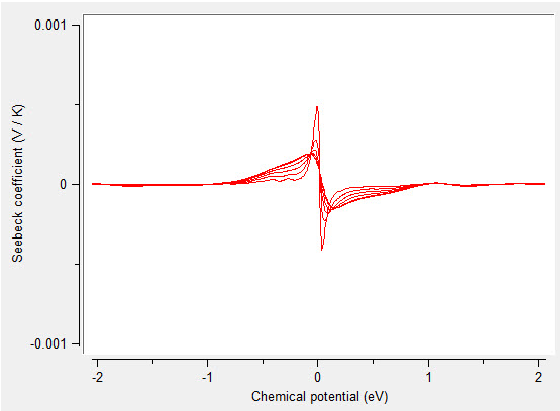
Figure 20.3.3 Thermoelectric power of doped Bi2Te3 as a function of a simulated rigid band shift mimicking the doping. Different curves correspond to different temperatures.
Worth mentioning are the positive and negative values for p- and n-type doping as well as the strong peaks for small doping at low temperatures. In contrast, for increased doping the values level off considerably.
In Figure 20.3.4, the Seebeck coefficient at room temperature is displayed for a reduced doping range.
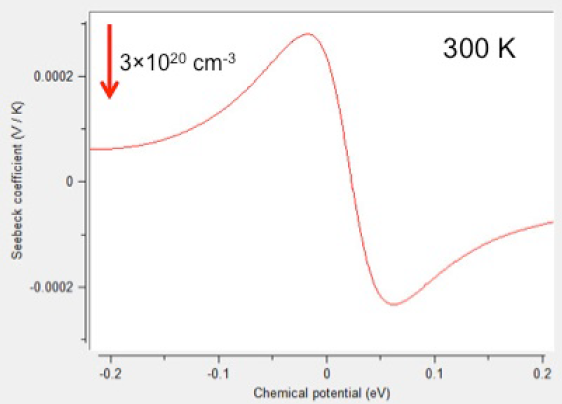
Figure 20.3.4 Thermoelectric power of doped Bi2Te3 as a function of a simulated rigid band shift mimicking the doping at a temperature of 300 K.
The red arrow indicates the doping obtained for that particular shift of the chemical potential. However, note that the doping bears a non-linear dependence on the shift of chemical potential, which depends on the details of the band structure.
The values of the Seebeck coefficient calculated for 300 K range from -220 \(\mu\)V/K (for n-type doping) to +300 \(\mu\)V/K (for p-type doping). Experimental values are rather rare and turned out to be strongly depending on the preparation conditions. For the bulk material they range from -250 \(\mu\)V/K (at an n-type doping concentration of 7.4 × 1018 cm-3) to +260 \(\mu\)V/K (at a p-type doping concentration of 4 × 1018 cm-3) [7], [8], [9]. In contrast, for n-doped thin films values ranging from -200 \(\mu\)V/K to -250 \(\mu\)V/K were reported [10].
20.4. Conclusion
First principles calculations of the thermoelectric properties on the basis of Boltzmann transport theory using MedeA VASP and MedeA Electronics are available as a routine application of the MedeA computational environment. Calculations for the prototype material Bi2Te3 have demonstrated the very good agreement of calculated values with experimental data and thereby confirmed the high predictive power of atomistic simulations for the determination of transport properties.
MedeA modules used in this application
- MedeA Environment
- MedeA VASP
- MedeA Electronics
| [1] | P. B. Allen, “Boltzmann Theory and Resistivity of Metals” in: “Quantum Theory of Real Materials”, edited by J. R. Chelikowsky and S. G. Louie (Kluwer, Boston, 1996), pp. 219-250. |
| [2] | T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding, and J. O. Sofo, “Transport coefficients from first-principles calculations”, Phys. Rev. B 68, 125210 (2003) (DOI) |
| [3] | G. K. H. Madsen and D. J. Singh, “BoltzTraP. A code for calculating band-structure dependent quantities”, Comput. Phys. Commun. 175, 67 (2006) (DOI) |
| [4] | A. Maignan, V. Eyert, C. Martin, S. Kremer, R. Frésard, and D. Pelloquin, Electronic structure and thermoelectric properties of CuRh1-xMgxO2”, Phys. Rev. B 80, 115103 (2009) (DOI) |
| [5] | V. Eyert, “The Augmented Spherical Wave Method”, Lect. Notes Phys. 849 (Springer, Berlin Heidelberg, 2013) (DOI) |
| [6] | (1, 2) G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”, Phys. Rev. B 54, 11169 (1996) (DOI); “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set”, Comput. Mater. Sci. 6, 15 (1996) (DOI) |
| [7] | (1, 2) R. Sehr and L. R. Testardi, “The optical properties of p-type Bi2Te3-Sb2Te3 alloys between 2-15 microns”, J. Phys. Chem. Solids 23, 1219 (1962) (DOI) |
| [8] | (1, 2) H. J. Goldsmid, “Thermoelectric Refrigeration”, (Springer, New York, 1964) (DOI) |
| [9] | J. Tan, K. Kalantar-zadeh, W. Wlodarski, S. Bhargava, D. Akolekar, A. Holland, and G. Rosengarten, “Thermoelectric properties of bismuth telluride thin films deposited by radio frequency magnetron sputtering”, Proc. SPIE 5836, “Smart Sensors, Actuators, and MEMS II”, 711 (2005) (DOI) |
| [10] | J. P. Carmo, L. M. Goncalves, and J. H. Correia, “Improved p- and n-type thin-film microstructures for thermoelectricity”, Electronics Lett. 45, 803 (2009) (DOI) |
| download: | pdf |
|---|