33. Thermostating Small-Molecule Systems
33.1. Introduction
The behavior of systems containing small molecules (diatomic/triatomic), in molecular simulations, is often affected by artifacts related to energy distribution. One such artifact, referred to as the “flying ice-cube” [1], leads to a violation of the equipartition of energy. This artifact significantly impacts the structural and dynamic properties of the system. To prevent such artifacts, different thermostats have been discussed in the literature [1] [2] [3] [4].
This application note focuses on the use of a simple thermostatting protocol that allows to quickly and efficiently achieve equipartition of energy. This protocol involves using the Nose-Hoover (NH) thermostat [6] [7] with a periodic redraw of velocities, similar to the Andersen “massive stochastic collisions” method [8] [9] and hence is referred to herein as the Nose-Hoover-Andersen (NHA) thermostat.
As a case study, we compute the density of pure compounds (diatomic/triatomic molecules) as a function of pressure. We present the computed energy partition between the translational, rotational, and vibrational degrees of freedom (DoF) for a system of diatomic molecules (oxygen), when different thermostats are employed. The results demonstrate that the NHA thermostat achieves equipartition of energy very rapidly for systems with low to high density (0.05-0.5 g/ml). The higher the density, the faster energy equipartition is achieved.
Key benefits of the NHA thermostat for equilibration
- a very rapid equilibration of the system to reach energy equipartition, for low to high density systems (> 0.05 g/ml),
- an easy implementation without the need to use additional parameters,
- general applicability to systems containing any number of small/large molecules and solids,
- no additional computational cost compared to the use of the NH thermostat
33.2. Diatomic & Triatomic Molecules
Diatomic molecules, such as nitrogen (N2) and oxygen (O2), have three translational, two rotational, and one vibrational DoF, leading to a total of six DoF. According to the equipartition theorem, the energy associated with these DoF is distributed evenly, resulting in an average energy of \((6/2)kT\) per molecule.
Triatomic molecules, such as CO2, H2O, H2S, SO2, possess three translational, three rotational, and up to three vibrational DoF, depending on the molecular structure. This results in a total of up to nine DoF, leading to an average energy of up to \((9/2)kT\).
Equipartition of Energy
The equipartition theorem states that, at thermal equilibrium, the total energy of a system is equally distributed among its DoF. For a system of classical particles, each DoF contributes an average energy of \((1/2)kT\), where \(k\) is the Boltzmann constant and \(T\) is the absolute temperature. The implications of equipartition extend beyond mere energy distribution; they also influence the thermodynamic properties of substances, such as heat capacity and phase transitions, making it a cornerstone of thermodynamic theory.
33.3. Thermostats in molecular dynamics
In molecular dynamics simulations, thermostats are employed to control the temperature of the system and ensure that the energy distribution aligns with the principles of equipartition. Thermostats can be classified into several categories, including deterministic, stochastic, and hybrid methods. Each type of thermostat has its own advantages and limitations, which can significantly impact the accuracy of energy distribution in simulations. The choice of thermostat is not merely a technical detail; it can fundamentally alter the dynamics of the system being studied, influencing the outcomes of simulations in fields ranging from drug design to materials science.
33.4. Case study: Densities of O2, H2, N2, CO2, CH4
We present density calculations for several small diatomic and triatomic molecules using a consistent computational protocol. Density isotherms at 298 K are determined through pressure-loop simulations on systems containig 500 molecules. The density of the initial configurations is set to 0.05 g/ml. Each simulation consists of short NVT and NPT equilibration stages followed by a production NPT stage employing the NH thermostat. To investigate the impact of equilibration on the computed density, we compare results from two sets of calculations differing in the equilibration thermostat used: NHA for the first set and NH for the second. While density equilibration occurrs within 100-200 ps with the NHA/NH protocol, several nanoseconds are required when using the NH/NH protocol. Consequently, production runs are set to 1 ns and 10-20 ns for the NHA/NH and the NH/NH protocols, respectively.
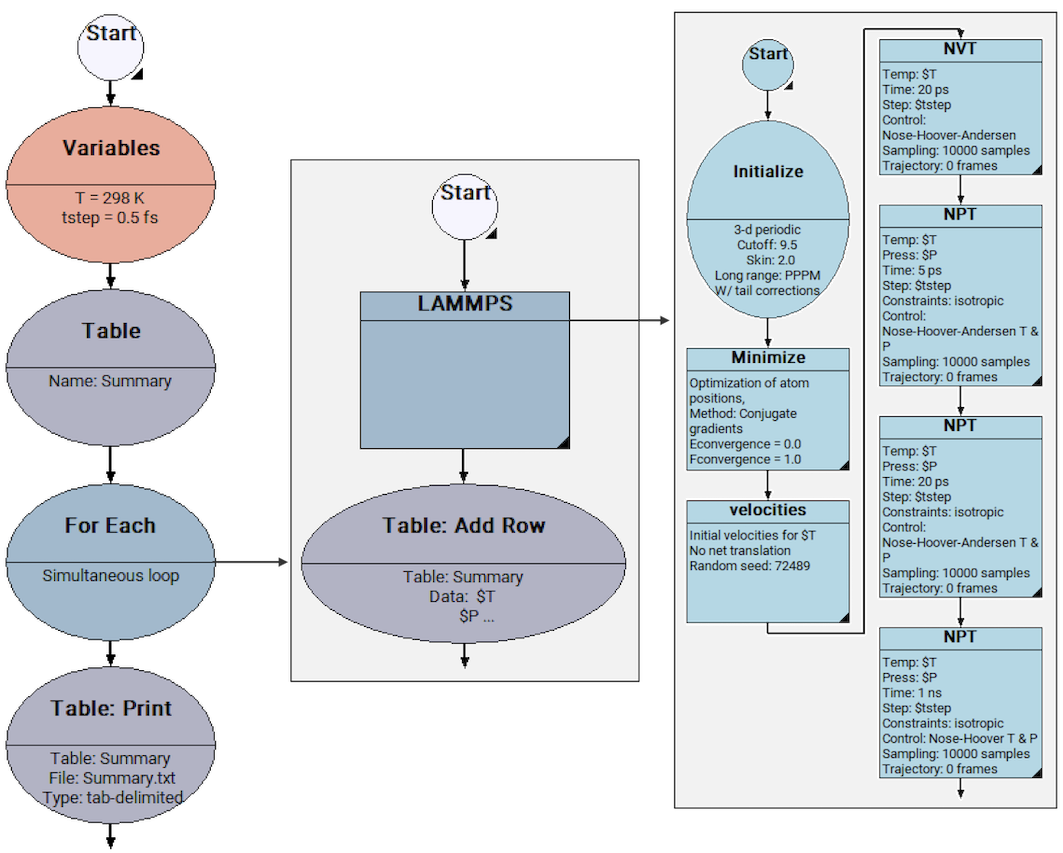
Figure 33.4.1 Flowchart used for the computation of density as a function of pressure, at T = 298 K. The “For Each” stage is used for looping over many values of pressure. At each pressure, an MD simulation takes place, including a short equilibration NVT stage (20 ps), two short equilibration NPT stages (5 ps / 20 ps) and then a production NPT stage (1 ns).
In Figure 33.4.2 we can see that for all systems, at all state points studied, we can observe an excellent agreement of results obtained from MD simulations with the NIST correlations, when the NHA/NH protocol is being used. However, important deviations of simulations results from NIST correlations may be present when the NH/NH protocol is used, particularly for H2 and CO2.
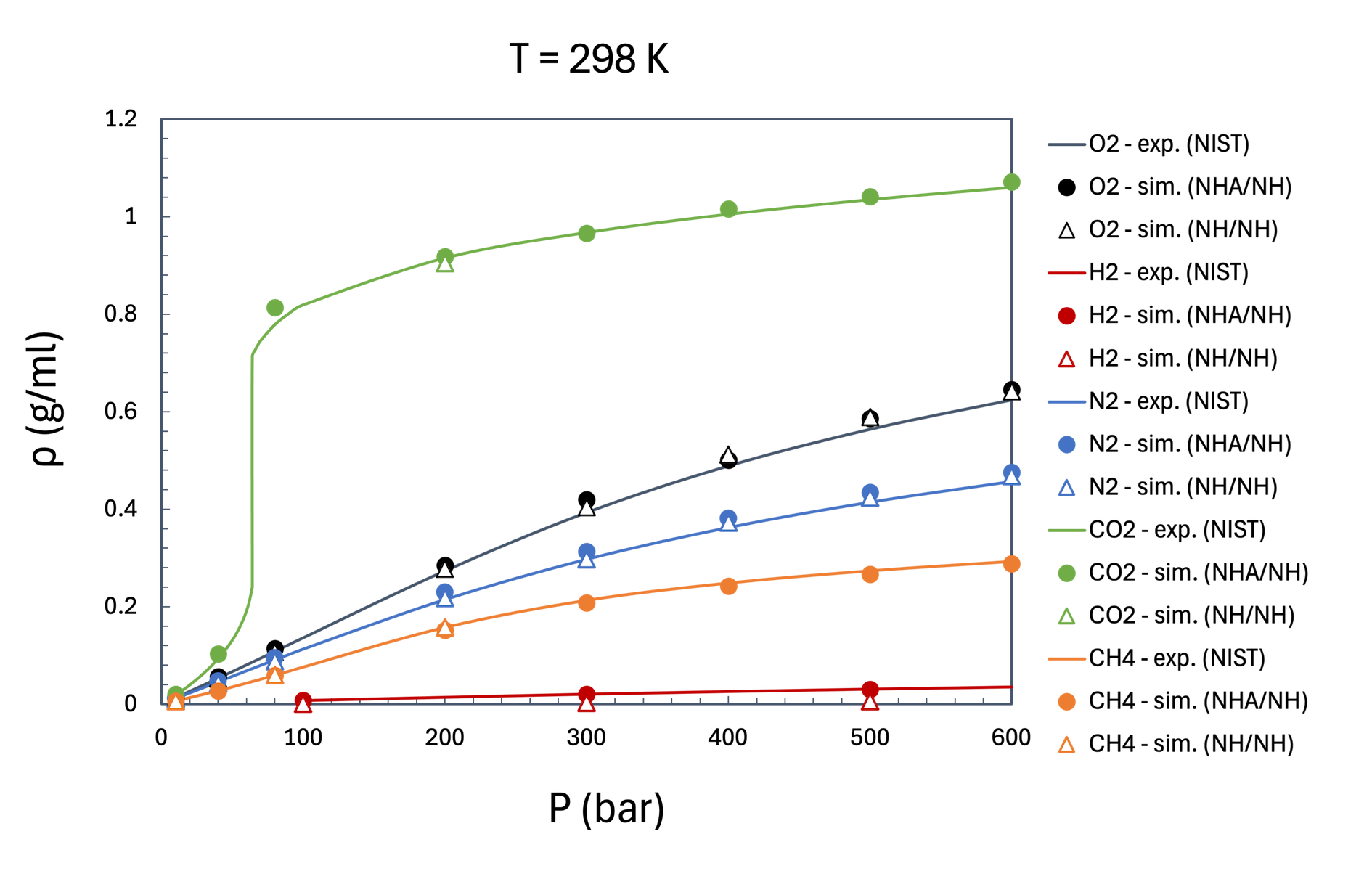
Figure 33.4.2 Density as a function of pressure for several small molecules: O2, H2, N2, CO2, CH4 at 298 K. Full lines represent NIST data [5], full symbols represent simulation results using the NHA/NH thermostatting protocol, and open symbols represent simulation results using the NH/NH thermostating protocol.
It is worth noting, that even when NH/NH density predictions closely match NIST data, we suspect inaccurate system dynamics in cases where energy equipartition is not respected. One such example is illustrated in the rest of this note, for O2, where while the density computed using the NH/NH protocol seems to be in good agreement with NIST data, the energy partitioning is skewed when using the NH thermostat for equilibration. The same can be observed when using the simple velocity rescaling (SVR) and the Berendsen thermostats. Energy is drained from high-frequency DoF in favor of low-frequency DoF. This is expected to directly impact properties such as diffusivity, thermal conductivity, and heat capacity.
33.5. Partitioning of energy for O2 systems
Here, we study the partition of energy for systems of pure O2during NVT simulations at low density (0.05 g/ml) and at high density (0.5 g/ml), corresponding to ~38 and ~390 bar respectively. Oxygen, a diatomic molecule in an atomistic representation, is the simplest system that can be studied and as such it is useful for assessing the ability of different thermostats to achieve equipartition of energy. We follow the method used by Braun et al. [2] for computing the energy partitioning in NVT simulations, using the following thermostats: (1) simple velocity rescaling (SVR) [14], (2) Nose-Hoover (NH) [6] [7], (3) Berendsen [12], (4) Langevin [13], (5) canonical sampling velocity rescaling (CSVR) [10] [11] , and (6) Nose-Hoover-Andersen (NHA; this work). The NH thermostat is actually a chain NH thermostat (length = 3).
In Figure 33.5.1 we can see the partitioning of energy in the translational, rotational and vibrational degrees of freedom.
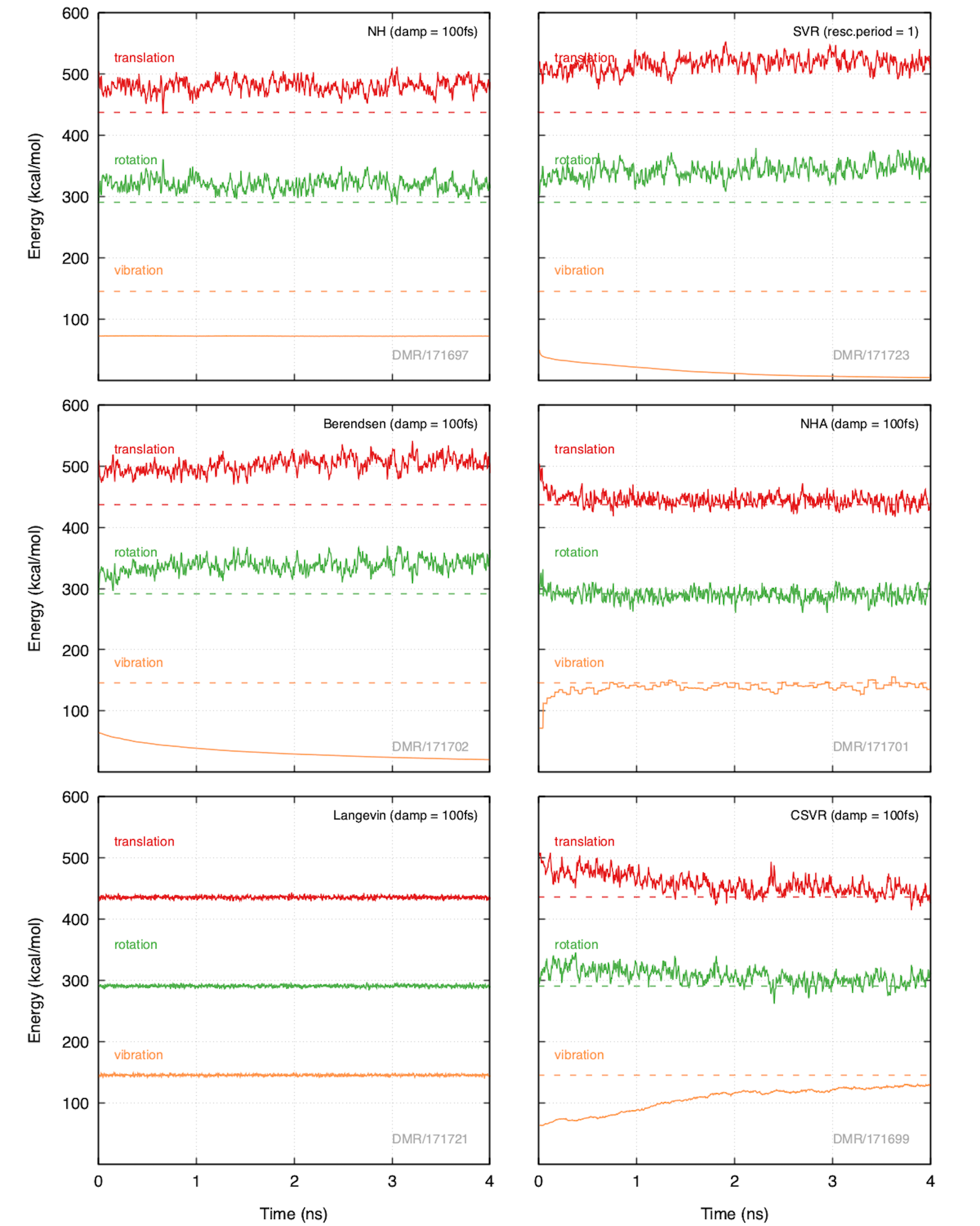
Figure 33.5.1 Partitioning of the kinetic energies obtained from MD simulations performed under the same conditions (500 O2 molecules, ρ = 0.05 g/ml, T = 293K, timestep = 0.5 fs). Full lines represent simulation output, while the dashed lines show the energy if equipartition is achieved. In all simulations shown, the COM momentum is fixed to zero.
As is shown in Figure 33.5.1, the NH, SVR and Berendsen thermostats all exhibit varying degrees of the “flying ice-cube” effect in the sense that kinetic energy is drawn from the high-frequency vibration mode and added to the rotational and translational modes. The SVR and Berendsen thermostats actually lead to a more pronounced effect for longer simulation times, i.e. move further away from equipartition continuously during the NVT simulation. The NH thermostat appears to not evolve with time but is more or less stuck at the same state during the entire 4 ns simulation duration. On the other hand, the NHA, and Langevin thermostats are able to achieve equipartition of energy and very quickly so. Specifically, the Langevin thermostat exhibits energy equipartition almost from the beginning of the simulation. The CSVR thermostat seems to move towards energy equipartition, however, at a slow pace; at 4 ns of simulation it seems that energy equipartition has not yet been completely achieved. It appears that Langevin and NHA are the best options for thermostatting the system towards equilibrium.
Focusing on the NHA thermostat used for equilibration, it appears that the choice of interval for the complete redrawing of velocities does affect the performance. More specifically, the lower the density, the larger the interval needs to be, thus leading to a need for longer equilibration times. As is shown in Figure 33.5.2 and Figure 33.5.3 at a density of 0.05 g/ml, the NHA interval for the complete redrawing of velocities should be ~20 ps while at a density of 0.5 g/ml ~2 ps suffice. That also means for higher densities a shorter equilibration run is needed compared to lower densities. It appears as the frequency of molecule collisions affects greatly the ability of the system and the thermostat to partition energy appropriately.
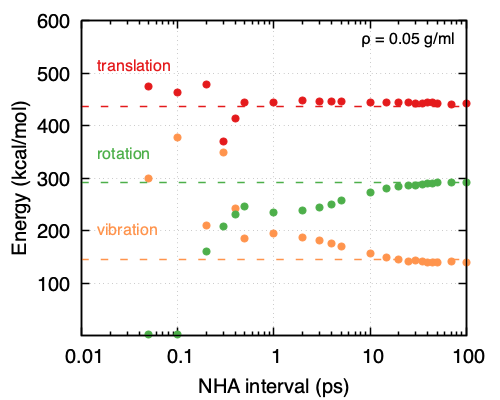
Figure 33.5.2 Partitioning of the kinetic energies obtained from MD simulations performed under the same conditions (NHA thermostat, 500 O2 molecules, ρ = 0.05 g/ml, T = 293K, timestep = 0.5 fs) and different intervals for reapplying the velocities to all the atoms in the system.
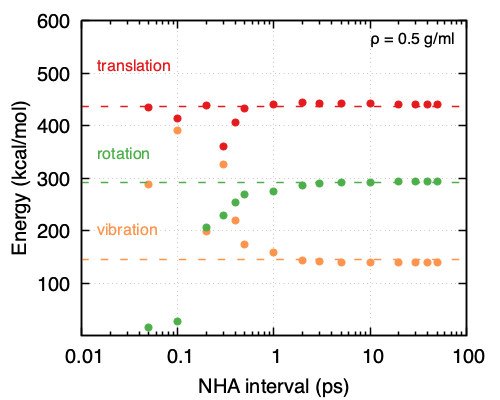
Figure 33.5.3 Partitioning of the kinetic energies obtained from MD simulations performed under the same conditions (NHA thermostat, 500 O2 molecules, ρ = 0.5 g/ml, T = 293K, timestep = 0.5 fs) and different intervals for reapplying the velocities to all the atoms in the system.
Thermostat for production runs
After equilibrium has been reached, NHA should be replaced by NH, for appropriate sampling and computation of structural and dynamic properties in a succeeding production run.
33.6. Conclusion
The use of different thermostats plays a crucial role in ensuring the equipartition of energy in systems containing small molecules, such as diatomic and triatomic species. Achieving energy equipartition is crucial for molecular dynamics simulations and for accurately modeling molecular behavior.
We have demonstrated in this note that a simple protocol that uses the NHA thermostat for a short equilibrium period (a few tens of ps) followed by an NPT production stage of no more than a few hundred ps suffices to equilibrate a system of pure compounds at its appropriate density. Equipartition of energy is achieved very quickly during the short initial NVT equilibration stage.
33.7. Future Directions
Extending this study to systems with both small and large molecules (e.g. O2 in a polymer) would be of interest. Oftentimes, rigid bodies are used for small molecules in such systems, possibly for avoiding such issues and artifacts. However, thermostatting systems containing both rigid and flexible molecules is not trivial and best avoided. Preliminary results suggest that the use of the NHA thermostat protocol is useful and efficient also in such systems.
Required Modules
- MedeA Environment including the modules Molecular Builder, LAMMPS, LAMMPS GUI, Forcefield Bundle and job control (JobServer and TaskServer)
- MedeA Amorphous Materials Builder
| [1] | (1, 2) Harvey et al., J. Comput. Chem. 19 (7), 726-740 (1998) |
| [2] | (1, 2) Braun et al., J. Chem. Theory Comput. 14, 5262-5272 (2018) |
| [3] | Olarte-Plata et al., Mol. Sim. 48 (1), 87-98 (2022) |
| [4] | Halonen et al., J. Chem. Phys. 158, 194301 (2023) |
| [5] | NIST Chemistry WebBook, SRD 69, https://webbook.nist.gov/chemistry/fluid/ |
| [6] | (1, 2) Nose, Mol. Phys 52, 255-268 (1984) |
| [7] | (1, 2) Hoover, Phys. Rev. A 31, 1695–1697 (1985) |
| [8] | Andersen, J. Chem. Phys. 72, 2384–2393 (1980) |
| [9] | Andrea et al., J. Chem. Phys. 79, 4576-4584 (1983) |
| [10] | Bussi et al., J. Chem. Phys. 126, 014101 (2007) |
| [11] | Heyes, Chem. Phys. 82, 285–301 (1983) |
| [12] | Berendsen et al., J. Chem. Phys. 81, 3684–3690 (1984) |
| [13] | Schneider et al., Phys. Rev. B 17, 1302 (1978) |
| [14] | Woodcock, Chem. Phys. Lett. 10, 257–261 (1971) |
| download: | pdf |
|---|