21. Accurate Band Gaps of Correlated Transition-Metal Oxides from Hybrid-Functional Calculations
The electronic structures of the metallic and insulating phases of VO2are calculated using density functional theory and modern hybrid functionals as implemented in MedeA®[1] VASP. Strongly contrasting previous calculations as based on local or semilocal approximations, which missed the insulating behavior of the low-temperature phase, these refined approaches accurately reproduce the optical band gap and thus bring to an end a fifty-year old controversy on the origin of the metal-insulator transition of VO2.
Keywords: Transition-metal oxides, vanadium dioxide, metal-insulator transition, electron correlations, optical band gap, MedeA, VASP, hybrid functionals
21.1. Background
The metal-insulator transition (MIT) of stoichiometric VO2at ambient pressure has been the subject of ongoing dispute since its discovery in the 1950s [2] [3]. Occurring at a technologically interesting temperature of 340 K this metal-insulator transition is connected with a change in resistivity of several orders of magnitude. Interestingly, it is also closely tied to a structural transition from the high-temperature rutile structure to a low-temperature monoclinic M1 structure, which deviates from the former by a pronounced V-V dimerization parallel to the rutile c-axis and a zigzag-like antiferroelectric displacement of the V atoms perpendicular to this axis.
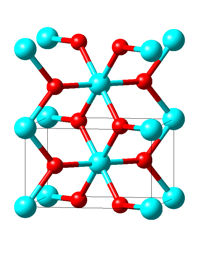
Figure 21.1.1 High-temperature rutile structure of VO2.Vanadium and oxygen atoms are given in cyan and red, respectively.
In Figure 21.1.1, two unit cells of the rutile structure with the characteristic VO6 octahedra and the vertical V-atom chains are displayed. In the monoclinic M1 structure shown in Figure 21.1.2 the unit cell is doubled and the vanadium atoms in the chains are dimerized as well as horizontally shifted off the octahedral centers.
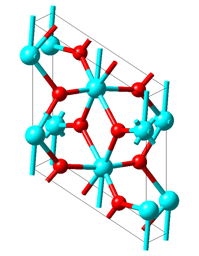
Figure 21.1.2 Low-temperature monoclinic M1 structure of VO2. Vanadium and oxygen atoms are given in cyan and red, respectively.
As has been worked out in detail by Goodenough, these atomic displacements can be nicely translated into energetic shifts and splittings of the relevant V 3d and closely related O 2p states. In doing so, Goodenough was indeed able to provide a qualitative understanding of the metal-insulator transition within the framework of an orbital or band picture [4], [5]. This was soon after questioned by Mott and coworkers, who were convinced that strong electron correlations play a dominant role for the metal-insulator transition and regarded the structural changes rather as an amendment [6]. Indeed, first principles calculations as based on density functional theory and the local density or generalized gradient approximation just missed the insulating behavior and resulted in a tiny semimetal-like overlap of the valence and conduction bands [3], [7]. The situation became even more complicated by the discovery of the additional low-temperature insulating M2phase with a slightly different pattern of the structural distortions and long-range magnetic ordering, which even more fired up the debate [8]. Again, density functional theory together with a semilocal approximation failed to correctly capture the insulating behavior [7].
This application note demonstrates the outstanding capability of the MedeA Environment with modern hybrid functionals as implemented in VASP [9] to accurately describe the electronic and magnetic properties of both the metallic and insulating phases of correlated electron materials and thereby to settle the long-standing dispute on the origin on the metal-insulator transition of the cornerstone material VO2[10].
21.2. Method of Calculation
While density functional theory is an exact theory for the ground state its practical application requires the specification of the unknown exchange-correlation functional. Local and semilocal approximations such as the local density approximation (LDA) and the generalized gradient approximation (GGA) have proven to be perfectly suited for describing rather weakly-correlated metals but are well known to underestimate or in some cases even miss the optical band gap of semiconductors and insulators. Developments to overcome this weakness led to the so-called hybrid functionals, which combine the local exchange with non-local contributions as known from Hartree-Fock theory. This approach yields very accurate band gaps for a vast number of semiconductors [11]. Specifically, in the present context we use the hybrid functional as proposed by Heyd, Scuseria, and Ernzerhof (HSE) [12].
21.3. Computed Results
The calculations were performed for both the metallic high-temperature rutile phase and the insulating low-temperature monoclinic M1 phase. The partial densities of states (DOS) calculated for the rutile phase using the GGA and HSE functional are displayed in Figure 21.3.1.
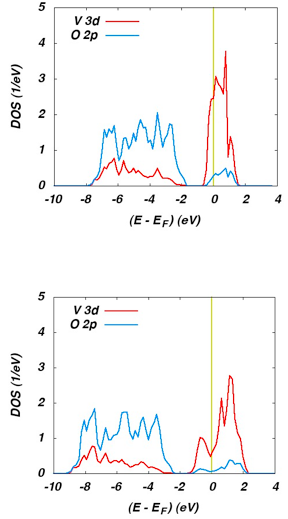
Figure 21.3.1 Partial DOS of rutile VO2as calculated using the GGA (top) and the HSE (bottom) functional.
The O 2p and V 3d states (with small admixtures from the respective other type of orbital due to hybridization of these states) are easily recognized well below and at the Fermi energy. Both functionals result in metallic behavior in accordance with the experimental findings. However, use of the hybrid functional leads to a much larger width of the V 3d bands in much better agreement with photoemission data.
The corresponding partial DOS for the monoclinic M1 phase are displayed in Figure 21.3.2. Again, the O 2p and V 3d states are well separated for both functionals. Yet, GGA and HSE result in completely different behavior. While the GGA leads to metallic behavior as clearly indicated by the presence of electronic states at the Fermi energy (see the blue arrow), the HSE calculations reproduce the observed optical band gap as likewise indicated by a blue arrow.
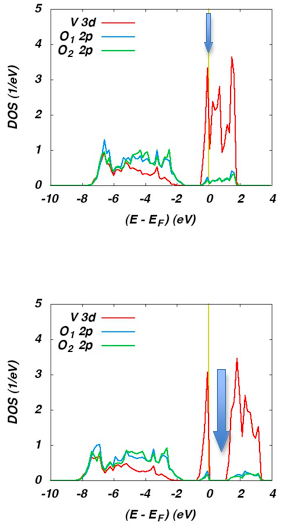
Figure 21.3.2 Partial DOS of M1-VO2as calculated using the GGA (top) and the HSE (bottom) functional.
Finally, spin-polarized antiferromagnetic calculations were performed for the insulating M2phase. While for this phase, GGA calculations likewise had failed to reproduce the insulting behavior, HSE calculations were successful in obtaining the optical band gap and well localized magnetic moments at the vanadium sites, thus impressively underlining the striking progress offered by the hybrid functionals.
21.4. Conclusion
First principles calculations using the recently developed hybrid functionals have been demonstrated to be well capable of fully describing the electronic and magnetic properties of the insulating phases of VO2, which is one of the key representatives of the broad class of so-called electronically correlated materials. Furthermore, the calculations allow for a deeper understanding of the origin of the metal-insulator transition, which is shown to be intimately connected to the structural changes occurring at the phase transition.
MedeA modules used in this application
- MedeA Environment
- MedeA VASP
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | F. J. Morin, “Oxides Which show a Metal-to-Insulator Transition at the Neel Temperature”, Phys. Rev. Lett. 3, 34 (1959) (DOI) |
| [3] | (1, 2) V. Eyert, “The metal-insulator transitions of VO2: A band theoretical approach”, Ann. Phys. (Leipzig) 11, 650 (2002) (DOI) |
| [4] | J. B. Goodenough, “Direct Cation-Cation Interactions in Several Oxides”, Phys. Rev. 117, 1442 (1960) (DOI) |
| [5] | J. B. Goodenough, “The two components in the crystallographic transition in VO2”, J. Sol. St. Chem. 3, 490 (1971) (DOI) |
| [6] | A. Zylbersztejn and N. F. Mott, “Metal-insulator transition in vanadium dioxide”, Phys. Rev. B 11, 4383 (1975) (DOI) |
| [7] | (1, 2) R. M. Wentzcovitch, W. W. Schulz, and P. B. Allen, “VO2: Peierls or Mott-Hubbard? A view from band theory”, Phys. Rev. Lett. 72, 3389 1994) (DOI); “Wentzcovitch et al. reply”, Phys. Rev. Lett. 73, 3043 1994) (DOI) |
| [8] | T. M. Rice, H. Launois, and J. P. Pouget, “Comment on “VO2: Peierls or Mott-Hubbard? A view from band theory”“, Phys. Rev. Lett. 73, 3042 1994) (DOI) |
| [9] | G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”, Phys. Rev. B 54, 11169 (1996) (DOI); “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set”, Comput. Mater. Sci. 6, 15 (1996) (DOI) |
| [10] | V. Eyert, “VO2: A Novel View from Band Theory”, Phys. Rev. Lett. 107, 016401(2011) (DOI) |
| [11] | M. Marsman, J. Paier, A. Stroppa, and G. Kresse, “Hybrid functionals applied to extended systems”, J. Phys.: Condens. Matter 20, 064201(2008) (DOI) |
| [12] | J. Heyd, G. E. Scuseria, and M. Ernzerhof, “Hybrid functionals based on a screened Coulomb potential”, J. Chem. Phys. 118, 8207 (2003) (DOI); “Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)]”, J. Chem. Phys. 124, 219906 (2006) (DOI) |
| download: | pdf |
|---|