MedeA MLP
At-a-Glance
MedeA®[1] MLP (Machine-Learned Potential) provides full MedeA support for LAMMPS based machine-learned potential simulations, including the simulation of mechanical, vibrational, and transport properties combined with comprehensive MedeA based analysis of simulation results.
MedeA MLP includes a library of published machine-learned potentials derived from different formalisms including the Spectral Neighbor Analysis Potential (SNAP) [2], Neural Network Potentials (NNP) [3], and the Atomic Cluster Expansion (ACE) [4], which are all supported by LAMMPS.
MedeA LAMMPS based simulations using MedeA MLP typically show excellent agreement with first-principles methods for systems that are well represented by the training set employed in creating the machine-learned potential.
Key Benefits
Productivity
- Extends ab initio simulation results to larger length and time scales through substantially reduced energy and force calculation times
- Efficient use of published machine-learned potentials
- Automates the handling of files and data for efficient simulation
Access
- Allows access to all MedeA LAMMPS simulation properties with machine-learned potential accuracy
- Can be employed with the Machine-Learned Potential Generator (MedeA MLPG) to access newly derived machine-learned potentials
- Handles diverse atomic geometries including making and breaking of bonds
Machine learning methods allow rich first-principles datasets to be mined and employed in interpolation and inference. Such techniques are having a dramatic effect in many areas of science. In materials science, they allow researchers to obtain the accuracy and freedom from bias of ab initio methods at reasonable computational cost for substantial simulation times and system sizes.
Machine learning based methods for energy and force calculation have been used for a number of years. For example, Blank et al. in 1995 employed a neural net based methodology to probe the energetics of CO on the Ni(111) surface [5]. In recent years it has become increasingly clear that such approaches, employing novel descriptors and advanced machine learning techniques, can yield exceptionally accurate reproduction of quantum mechanical training data at substantially reduced computational cost [6].
MedeA MLP provides easy to use and efficient access to such methods. By making such machine-learned potentials accessible for use with MedeA LAMMPS, MedeA MLP extends the range of ab initio methods to much larger length and time scales, while relying on first-principles results for accuracy and validation. All input data and necessary files are readily accessible using the MedeA JobServer infrastructure.
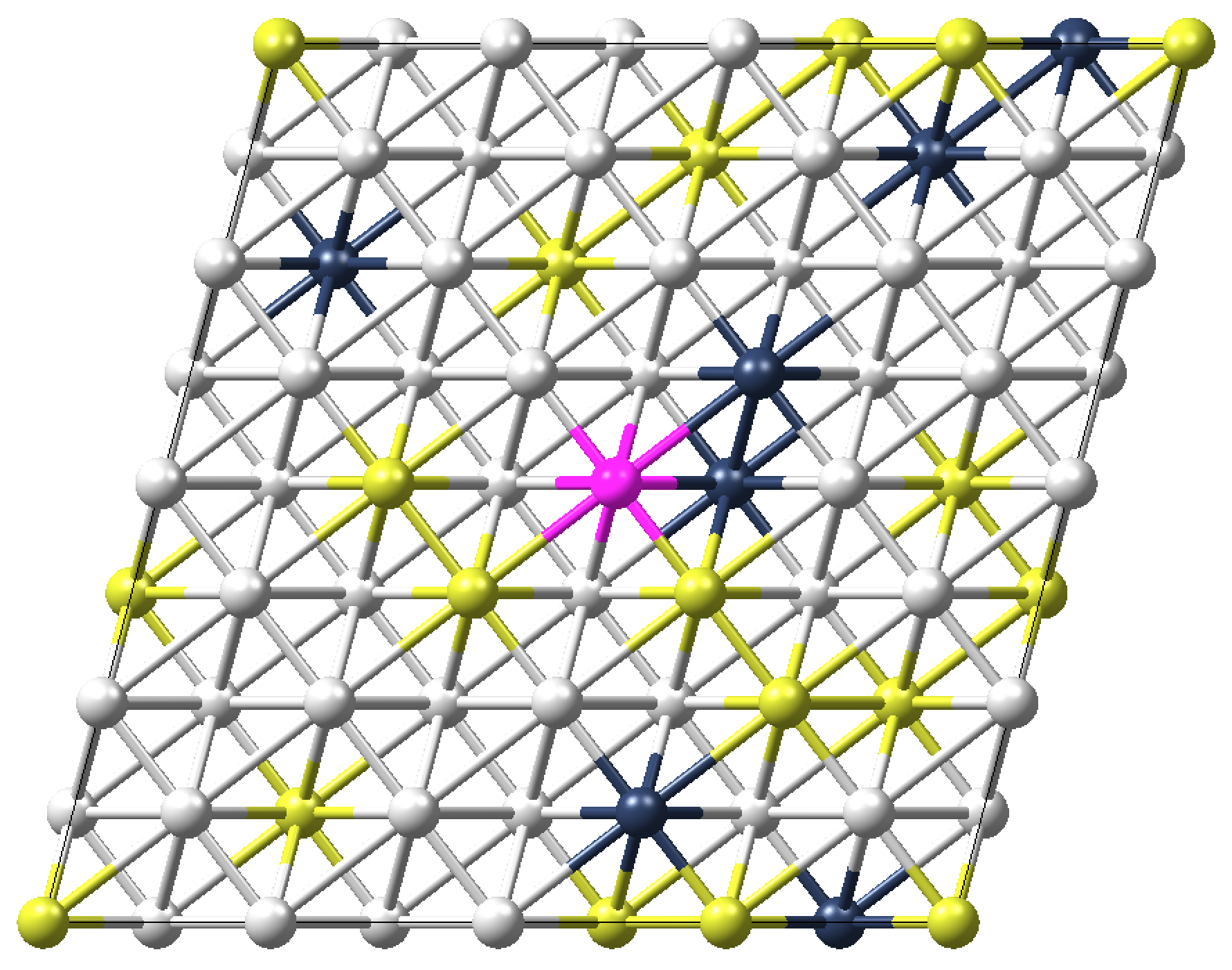
Machine-learned potential simulations are based on descriptors of the local atomic environment within a defined cutoff radius. These descriptors are employed, via machine learning based training, to compute the energy of the complete system as a sum of atomic contributions. This image displays the local cluster of an atom.
Technical Features
User Interface
- Import MLPs .frc files
- Automatic atom type assignment
- Automated creation of LAMMPS input datasets
Example Systems
- Cu, Ge, Li, Mo, Ni, Si, Ta, W
- InP, Li3N, NbMoTaW, NiMo, WBe
Key Features
- Library of published machine-learned potentials
- Full support for the SNAP description
- Enables LAMMPS MLP simulations in the MedeA Environment
Required Modules
- MedeA Environment
- MedeA LAMMPS
Find Out More
Learn more about Machine Learning by watching the webinar: https://www.materialsdesign.com/webinars/recorded/mlp-surpassing-the-limits-of-ab-initio
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles, and G. J. Tucker, Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials, J. Comp. Phys. 285, 316 (2015) (DOI) |
| [3] | A. Singraber, J. Behler and C. Dellago, Library-Based LAMMPS Implementation of High-Dimensional Neural Network Potentials, J. Chem. Theory Comput. 15, 1827-1840 (2019) (DOI) |
| [4] | R. Drautz, Atomic cluster expansion for accurate and transferable interatomic potentials, Phys. Rev. B, 99(1), 014104 (2019) |
| [5] | T. B. Blank, S. D. Brown, A. W. Calhoun, D. J. Doren, Neural network models of potential energy surfaces, J. Chem. Phys., 103, 4129 (1995) |
| [6] | J. Behler, and M. Parrinello, Generalized neural-network representation of high-dimensional potential energy surfaces, Phys. Rev. Lett. 98, 146401 (2007) |
| download: | pdf |
|---|