MedeA Crystal Morphology - From Atomic Arrangement to Crystal Shape

At-a-Glance

MedeA®[1] Crystal Morphology employs lattice parameters and space-group symmetry as well as information on relative surface stabilities to simulate the morphology of a crystal.

Key Benefits

  • Interactive determination of the morphology

  • Highly flexible choice of different models of relative surface stabilities

When crystals are grown under equilibrium conditions, their macroscopic shape or morphology is determined by the minimum of the total surface free energy of the crystal, which in turn is governed by the microscopic interatomic forces. Since the latter are accessible to atomistic simulations, first-principles calculations of morphologies have become the method of choice to predict crystal morphologies.

At the same time, macroscopically observed morphologies of crystals and crystallites provide insight into the details of materials at the microscopic levels. In particular, scanning electron microscopy (SEM) images, as widely employed in the analysis of materials samples, reveal information on the morphology adopted by individual crystallites.

MedeA Crystal Morphology combines the lattice parameters and space-group-symmetry of a crystal with information about the relative energies of low-index crystal faces to simulate the morphology. As originally proposed by Wulff, the length of a surface normal from a given crystal face to a common point within the crystal interior is proportional to its surface energy [2]. Indeed, a crystal shape constructed in this manner minimizes its surface free energy.

The relative stabilities of crystal faces enter via a set of rules proposed by Bravais, Friedel, Donnay and Harker [3],[4] [5]. Alternatively, computed or measured surface energies can be used.

As an example, the morphology of Cr2O3 is displayed in the figure below. It is based on lattice parameters and space-group symmetry as provided by MedeA InfoMaticA as well as surface energies reported by Davies et al. [6]. As expected, the computed morphology reflects the rhombohedral shape of the corundum structure.

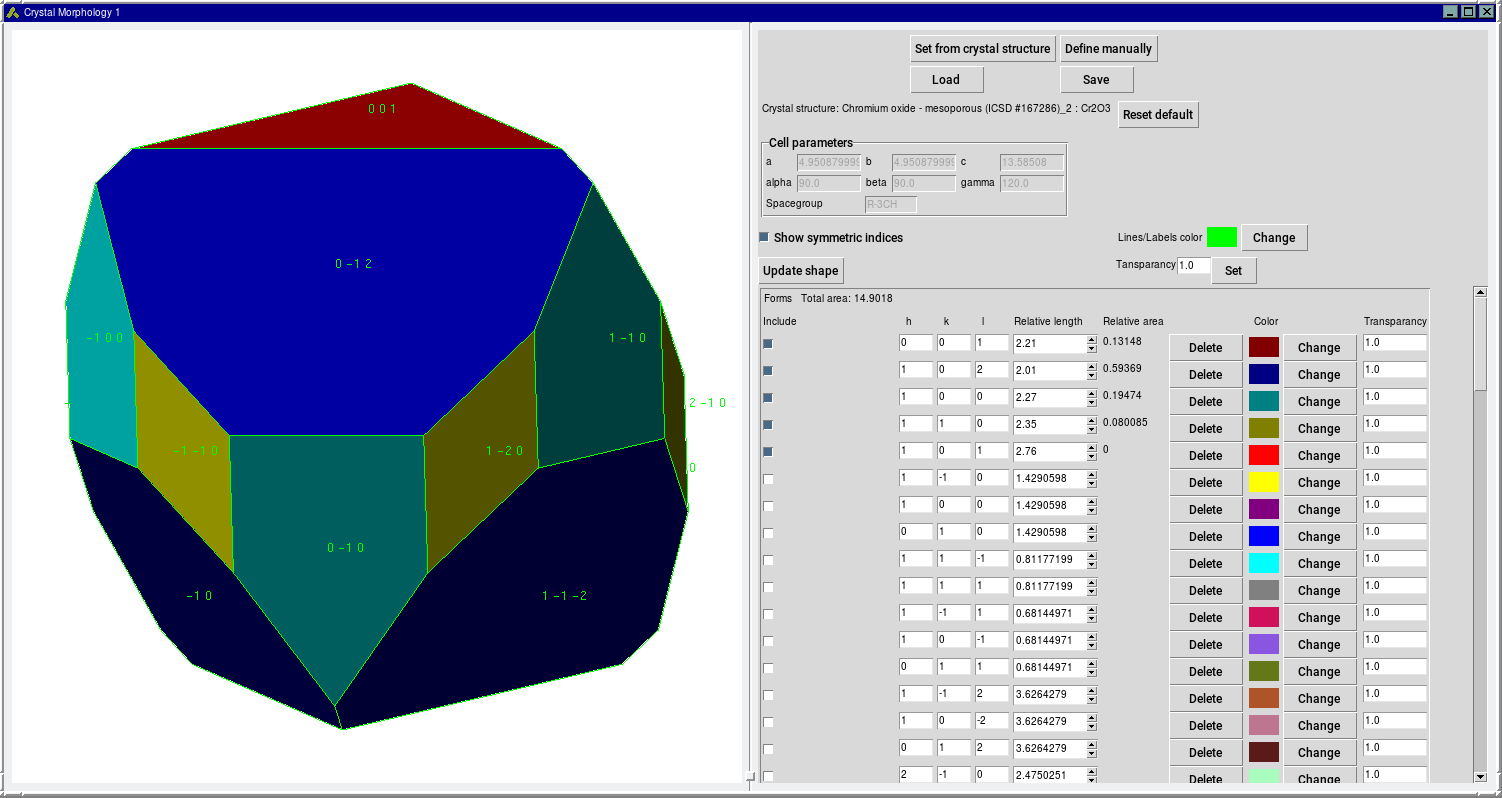
../_images/Morphology-Cr2O3-ICSD167286.png

MedeA Crystal Morphology Screenshot: Morphology of Cr2O3 as based on reported surface energies [6]

Key Features

  • An intuitive user interface for the generation of morphologies using lattice parameters and space-group symmetry as input

  • Full integration with MedeA InfoMaticA

  • Uses Wulff construction for morphology generation

  • Relative surface stabilities are automatically determined from the rules introduced by Bravais, Friedel, Donnay and Harker

  • Alternatively, computed or measured surface energies can be employed

  • Morphology files can be saved for later use

  • Optimal graphical representation of results through a variety of visualization options

../_images/Morphology-Nano-Builder-Ti.png

The morphology of titanium metal and a nano-scale atomic model, containing 24,840 atoms, constructed using MedeA Crystal Morphology.

Model Building

MedeA Crystal Morphology provides model construction capabilities. For any given crystallite morphology, the MedeA Surface Builder can be invoked through a right-click context menu option, facilitating efficient atomic model construction based on crystallite surfaces.

Additionally, nano-scale crystallite atomic models may be constructed using MedeA Crystal Morphology.

Properties

  • Morphology of arbitrary crystals

Required Modules

  • MedeA Environment

  • MedeA Morphology

Find Out More

download:

pdf